Notes on Binius (Part II): Subspace Polynomial
FRI-Binus 论文 [DP24] 中讨论了基于 Subspace Polynomial 的 Additive FFT 算法,并给出了用奇偶项分解的视角来理解 [LCH14] 中的基于 Novel Polynomial Basis 的 Additive FFT 算法。本文直接介绍子空间多项式 Subspace Polynomial,然后据此介绍奇偶项分解视角的 Additive FFT 算法。本文省去了 Normalized Subspace Polynomial 的定义,方便读者理解。Normalization 只是影响 FFT 算法的性能,和本文介绍的简化版算法并没有本质的区别。
由于 Additive FFT 依赖的代数结构和素数域上的 Multiplicative FFT 非常相似,因此关于 Multiplicative FFT 的知识将有助于理解本文的内容。
线性子空间多项式 Subspace Polynomial ¶ 我们继续探索基于 F 2 \mathbb{F}_2 F 2 F 2 m \mathbb{F}_{2^m} F 2 m F 2 m \mathbb{F}_{2^m} F 2 m V m V_m V m ( β 0 , β 1 , … , β m − 1 ) (\beta_0, \beta_1, \ldots, \beta_{m-1}) ( β 0 , β 1 , … , β m − 1 ) V m = S p a n ( β 0 , β 1 , … , β m − 1 ) V_m=\mathsf{Span}(\beta_0, \beta_1, \ldots, \beta_{m-1}) V m = Span ( β 0 , β 1 , … , β m − 1 ) ⟨ ⋯ ⟩ \langle \cdots \rangle ⟨ ⋯ ⟩
V m = ⟨ β 0 , β 1 , … , β m − 1 ⟩ V_m = \langle \beta_0, \beta_1, \ldots, \beta_{m-1} \rangle V m = ⟨ β 0 , β 1 , … , β m − 1 ⟩ 这样任意一个元素 θ ∈ F 2 m \theta\in\mathbb{F}_{2^m} θ ∈ F 2 m
θ = c 0 ⋅ β 0 + c 1 ⋅ β 1 + … + c m − 1 ⋅ β m − 1 , where c i ∈ F 2 \theta = c_0\cdot \beta_0 + c_1\cdot \beta_1 + \ldots + c_{m-1}\cdot \beta_{m-1}, \text{ where $c_i\in \mathbb{F}_2$} θ = c 0 ⋅ β 0 + c 1 ⋅ β 1 + … + c m − 1 ⋅ β m − 1 , where c i ∈ F 2 同时 V m V_m V m V 0 = { 0 } V_0=\{0\} V 0 = { 0 } V k V_k V k V m V_m V m V k V_k V k V m V_m V m V k V_k V k V k V_k V k s k ( X ) s_k(X) s k ( X )
s k ( X ) = ∏ i = 0 2 k − 1 ( X − θ i ) , where θ i ∈ V k s_k(X) = \prod_{i=0}^{2^k-1}(X-\theta_i), \text{ where $\theta_i\in V_k$ } s k ( X ) = i = 0 ∏ 2 k − 1 ( X − θ i ) , where θ i ∈ V k 多项式 s k ( X ) s_k(X) s k ( X ) V k V_k V k θ ∈ V k \theta\in V_k θ ∈ V k
s k ( θ ) = 0 s_k(\theta) = 0 s k ( θ ) = 0 Linearized Polynomial ¶ 上面介绍的 Subspace 多项式是一种所谓的 Linearized Polynomial,因为它的定义满足下面的形式:
L ( X ) = ∑ i = 0 n − 1 c i ⋅ X q i , c i ∈ F q L(X) = \sum_{i=0}^{n-1} c_i\cdot X^{q^i}, \quad c_i\in \mathbb{F}_{q} L ( X ) = i = 0 ∑ n − 1 c i ⋅ X q i , c i ∈ F q 多项式 L ( X ) L(X) L ( X ) L ( X ) L(X) L ( X ) F q \mathbb{F}_{q} F q K K K L ( X ) L(X) L ( X ) K = F q s K=\mathbb{F}_{q^s} K = F q s θ ∈ K \theta\in K θ ∈ K L ( θ ) ∈ K L(\theta)\in K L ( θ ) ∈ K θ ≠ θ ′ \theta\neq\theta' θ = θ ′ L ( θ ) ≠ L ( θ ′ ) L(\theta)\neq L(\theta') L ( θ ) = L ( θ ′ ) L ( X ) L(X) L ( X ) B ∈ F q s × s B\in \mathbb{F}_q^{s\times s} B ∈ F q s × s F q s \mathbb{F}^s_q F q s
( c 0 , c 1 , … , c s − 1 ) B = ( d 0 , d 1 , … , d s − 1 ) (c_0, c_1, \ldots, c_{s-1}) B = (d_0, d_1, \ldots, d_{s-1}) ( c 0 , c 1 , … , c s − 1 ) B = ( d 0 , d 1 , … , d s − 1 ) 对于 Subspace Polynomial 而言,每一个 s k ( X ) s_k(X) s k ( X ) L ( X ) ∈ F q m [ X ] L(X)\in \mathbb{F}_{q^m}[X] L ( X ) ∈ F q m [ X ] V n ⊂ V m V_n\subset V_m V n ⊂ V m
线性性质 ¶ 由于 s k ( X ) s_k(X) s k ( X ) a i ⋅ X 2 i a_i\cdot X^{2^i} a i ⋅ X 2 i
s k ( x + y ) = s k ( x ) + s k ( y ) , ∀ x , y ∈ F 2 m s k ( c ⋅ x ) = c ⋅ s k ( x ) , ∀ x ∈ F 2 m , ∀ c ∈ F 2 \begin{align*}
s_k(x + y) &= s_k(x) + s_k(y), &\quad \forall x, y \in \mathbb{F}_{2^m}\\
s_k(c\cdot x) &= c\cdot s_k(x), &\quad \forall x\in \mathbb{F}_{2^m}, \forall c\in \mathbb{F}_2
\end{align*} s k ( x + y ) s k ( c ⋅ x ) = s k ( x ) + s k ( y ) , = c ⋅ s k ( x ) , ∀ x , y ∈ F 2 m ∀ x ∈ F 2 m , ∀ c ∈ F 2 我们来尝试简单证明第一个等式,根据有限域理论的一个常见定理(Freshman’s dream):
( x + y ) 2 = x 2 + 2 x y + y 2 = x 2 + y 2 , where x , y ∈ F 2 m (x + y)^{2} = x^2 + 2xy + y^2 = x^{2} + y^{2}, \quad\text{where $x, y\in \mathbb{F}_{2^m}$} ( x + y ) 2 = x 2 + 2 x y + y 2 = x 2 + y 2 , where x , y ∈ F 2 m 显然,2 x y = 0 2xy=0 2 x y = 0 2 = 0 2=0 2 = 0
( x + y ) 2 i = x 2 i + y 2 i (x + y)^{2^i} = x^{2^i} + y^{2^i} ( x + y ) 2 i = x 2 i + y 2 i 接下来验证下 s k ( X ) s_k(X) s k ( X )
s k ( x + y ) = ∑ i = 0 k a i ⋅ ( x + y ) 2 i = ∑ i = 0 k a i ⋅ ( x 2 i + y 2 i ) = s k ( x ) + s k ( y ) s_k(x + y) = \sum_{i=0}^{k} a_i\cdot (x+y)^{2^i} = \sum_{i=0}^{k} a_i\cdot \big(x^{2^i} + y^{2^i}\big) = s_k(x) + s_k(y) s k ( x + y ) = i = 0 ∑ k a i ⋅ ( x + y ) 2 i = i = 0 ∑ k a i ⋅ ( x 2 i + y 2 i ) = s k ( x ) + s k ( y ) 子空间多项式的递推式 ¶ 对于子空间 V k V_k V k
V k = V k − 1 ∪ ( β k − 1 + V k − 1 ) V_k = V_{k-1} \cup (\beta_{k-1}+V_{k-1}) V k = V k − 1 ∪ ( β k − 1 + V k − 1 ) 这里 V k = ⟨ β 0 , β 1 , … , β k − 1 ⟩ V_k=\langle \beta_0, \beta_1, \ldots, \beta_{k-1} \rangle V k = ⟨ β 0 , β 1 , … , β k − 1 ⟩ V k − 1 = ⟨ β 0 , β 1 , … , β k − 2 ⟩ V_{k-1}=\langle \beta_0, \beta_1, \ldots, \beta_{k-2} \rangle V k − 1 = ⟨ β 0 , β 1 , … , β k − 2 ⟩ V k V_k V k V k − 1 V_{k-1} V k − 1 β k − 1 + V k − 1 \beta_{k-1}+V_{k-1} β k − 1 + V k − 1
s k ( X ) = s k − 1 ( X ) ⋅ s k − 1 ( X + β k − 1 ) s_k(X) = s_{k-1}(X) \cdot s_{k-1}(X+\beta_{k-1}) s k ( X ) = s k − 1 ( X ) ⋅ s k − 1 ( X + β k − 1 ) 举个简单例子,假设 k = 3 k=3 k = 3 V 3 = ⟨ β 0 , β 1 , β 2 ⟩ V_3=\langle \beta_0,\beta_1,\beta_2\rangle V 3 = ⟨ β 0 , β 1 , β 2 ⟩ V 2 = ⟨ β 0 , β 1 ⟩ V_2=\langle \beta_0,\beta_1\rangle V 2 = ⟨ β 0 , β 1 ⟩ V 2 V_2 V 2 β 2 {\color{blue}\beta_2} β 2 V 3 V_3 V 3 2 2 + 2 2 = 8 2^2 + 2^2 = 8 2 2 + 2 2 = 8 V 3 V_3 V 3
V 3 = { 0 , β 0 , β 1 , β 0 + β 1 } ∪ { β 2 , β 0 + β 2 , β 1 + β 2 , ( β 0 + β 1 ) + β 2 } V_3 = \{0, \beta_0, \beta_1, \beta_0+\beta_1\} \cup \{{\color{blue}\beta_2}, \beta_0+{\color{blue}\beta_2}, \beta_1+{\color{blue}\beta_2}, (\beta_0+\beta_1)+{\color{blue}\beta_2}\} V 3 = { 0 , β 0 , β 1 , β 0 + β 1 } ∪ { β 2 , β 0 + β 2 , β 1 + β 2 , ( β 0 + β 1 ) + β 2 } 我们容易验证: s 3 ( X ) = s 2 ( X ) ⋅ s 2 ( X + β 2 ) s_3(X) = s_{2}(X) \cdot s_{2}(X+\beta_{2}) s 3 ( X ) = s 2 ( X ) ⋅ s 2 ( X + β 2 ) s 2 ( X ) s_{2}(X) s 2 ( X ) s 1 ( X ) s_1(X) s 1 ( X ) s 1 ( X + β 1 ) s_1(X+\beta_1) s 1 ( X + β 1 )
s 3 ( X ) = s 2 ( X ) ⋅ s 2 ( X + β 2 ) = s 2 ( X ) 2 + β 2 ⋅ s 2 ( X ) = s 1 ( X ) ⋅ s 1 ( X + β 1 ) ⋅ s 1 ( X ) ⋅ s 1 ( X + β 1 ) + β 2 ⋅ s 1 ( X ) ⋅ s 1 ( X + β 1 ) = ( s 1 ( X ) 2 + β 1 ⋅ s 1 ( X ) ) 2 + β 2 ⋅ s 1 ( X ) 2 + β 1 β 2 ⋅ s 1 ( X ) = s 1 ( X ) 4 + β 1 2 ⋅ s 1 ( X ) 2 + β 2 ⋅ s 1 ( X ) 2 + β 1 β 2 ⋅ s 1 ( X ) = s 1 ( X ) 4 + ( β 1 2 + β 2 ) ⋅ s 1 ( X ) 2 + β 1 β 2 ⋅ s 1 ( X ) = ( X ⋅ ( X + β 0 ) ) 4 + ( β 1 2 + β 2 ) ⋅ ( X ⋅ ( X + β 0 ) ) 2 + β 1 β 2 ⋅ ( X ⋅ ( X + β 0 ) ) = ( X 2 + β 0 ⋅ X ) 4 + ( β 1 2 + β 2 ) ⋅ ( X 2 + β 0 ⋅ X ) 2 + β 1 β 2 ⋅ ( X 2 + β 0 ⋅ X ) = X 8 + β 0 4 X 4 + ( β 1 2 + β 2 ) X 4 + β 0 2 ( β 1 2 + β 2 ) X 2 + β 1 β 2 X 2 + β 0 β 1 β 2 X \begin{split}
s_3(X) & = s_2(X)\cdot s_2(X + \beta_2) \\
& = s_2(X)^2 + \beta_2\cdot s_2(X) \\
& = s_1(X)\cdot s_1(X + \beta_1)\cdot s_1(X)\cdot s_1(X + \beta_1) + \beta_2\cdot s_1(X)\cdot s_1(X + \beta_1) \\
& = (s_1(X)^2 + \beta_1\cdot s_1(X))^2 + \beta_2\cdot s_1(X)^2 + \beta_1\beta_2\cdot s_1(X) \\
& = s_1(X)^4 + \beta_1^2\cdot s_1(X)^2 + \beta_2\cdot s_1(X)^2 + \beta_1\beta_2\cdot s_1(X) \\
& = s_1(X)^4 + (\beta_1^2+\beta_2)\cdot s_1(X)^2 + \beta_1\beta_2\cdot s_1(X) \\
& = (X\cdot(X+\beta_0))^4 + (\beta_1^2+\beta_2)\cdot (X\cdot(X + \beta_0))^2 + \beta_1\beta_2\cdot (X\cdot(X + \beta_0)) \\
& = (X^2 + \beta_0\cdot X)^4 + (\beta_1^2+\beta_2)\cdot (X^2 + \beta_0\cdot X)^2 + \beta_1\beta_2\cdot (X^2 + \beta_0\cdot X) \\
& = X^8 + \beta_0^4X^4 + (\beta_1^2+\beta_2)X^4 + \beta_0^2(\beta_1^2+\beta_2)X^2 + \beta_1\beta_2X^2 + \beta_0\beta_1\beta_2X \\
\end{split} s 3 ( X ) = s 2 ( X ) ⋅ s 2 ( X + β 2 ) = s 2 ( X ) 2 + β 2 ⋅ s 2 ( X ) = s 1 ( X ) ⋅ s 1 ( X + β 1 ) ⋅ s 1 ( X ) ⋅ s 1 ( X + β 1 ) + β 2 ⋅ s 1 ( X ) ⋅ s 1 ( X + β 1 ) = ( s 1 ( X ) 2 + β 1 ⋅ s 1 ( X ) ) 2 + β 2 ⋅ s 1 ( X ) 2 + β 1 β 2 ⋅ s 1 ( X ) = s 1 ( X ) 4 + β 1 2 ⋅ s 1 ( X ) 2 + β 2 ⋅ s 1 ( X ) 2 + β 1 β 2 ⋅ s 1 ( X ) = s 1 ( X ) 4 + ( β 1 2 + β 2 ) ⋅ s 1 ( X ) 2 + β 1 β 2 ⋅ s 1 ( X ) = ( X ⋅ ( X + β 0 ) ) 4 + ( β 1 2 + β 2 ) ⋅ ( X ⋅ ( X + β 0 ) ) 2 + β 1 β 2 ⋅ ( X ⋅ ( X + β 0 )) = ( X 2 + β 0 ⋅ X ) 4 + ( β 1 2 + β 2 ) ⋅ ( X 2 + β 0 ⋅ X ) 2 + β 1 β 2 ⋅ ( X 2 + β 0 ⋅ X ) = X 8 + β 0 4 X 4 + ( β 1 2 + β 2 ) X 4 + β 0 2 ( β 1 2 + β 2 ) X 2 + β 1 β 2 X 2 + β 0 β 1 β 2 X 最后 s 3 ( X ) s_3(X) s 3 ( X ) ∑ i = 0 k a i ⋅ X 2 i \sum_{i=0}^{k} a_i\cdot X^{2^i} ∑ i = 0 k a i ⋅ X 2 i
子空间上的同态映射 ¶ 因为 Subspace Polynomial 实际上是一种 Vanishing Polynomial,并且它还具有加法同态,所以我们可以利用 Subspace Polynomial 来定义子空间之间的同态映射。
例如对于 V 3 = ⟨ β 0 , β 1 , β 2 ⟩ V_3=\langle \beta_0, \beta_1, \beta_2\rangle V 3 = ⟨ β 0 , β 1 , β 2 ⟩ V 3 V_3 V 3 V 1 = { 0 , β 0 } V_1=\{0, \beta_0\} V 1 = { 0 , β 0 } s 1 ( X ) s_1(X) s 1 ( X )
s 1 ( X ) = X ⋅ ( X + β 0 ) s_1(X) = X\cdot (X+\beta_0) s 1 ( X ) = X ⋅ ( X + β 0 ) 很显然,s 1 ( V 1 ) = { 0 , 0 } s_1(V_1)=\{0, 0\} s 1 ( V 1 ) = { 0 , 0 } s 1 ( X ) s_1(X) s 1 ( X ) V 3 V_3 V 3
s 1 ( 0 ) = 0 s 1 ( β 0 ) = 0 s 1 ( β 1 ) = β 0 β 1 + β 1 2 s 1 ( β 0 + β 1 ) = β 0 β 1 + β 1 2 s 1 ( β 2 ) = β 0 β 2 + β 2 2 s 1 ( β 0 + β 2 ) = β 0 β 2 + β 2 2 s 1 ( β 1 + β 2 ) = β 0 β 1 + β 1 2 + β 0 β 2 + β 2 2 s 1 ( β 0 + β 1 + β 2 ) = β 0 β 1 + β 1 2 + β 0 β 2 + β 2 2 \begin{split}
s_1(0) &= 0\\
s_1(\beta_0) & = 0 \\
s_1(\beta_1) & = \beta_0\beta_1 + \beta_1^2\\
s_1(\beta_0+\beta_1) & = \beta_0\beta_1 + \beta_1^2\\
s_1(\beta_2) &= \beta_0\beta_2 + \beta_2^2\\
s_1(\beta_0+\beta_2) &= \beta_0\beta_2 + \beta_2^2\\
s_1(\beta_1+\beta_2) &= \beta_0\beta_1 + \beta_1^2 + \beta_0\beta_2 + \beta_2^2\\
s_1(\beta_0+\beta_1+\beta_2) &= \beta_0\beta_1 + \beta_1^2 + \beta_0\beta_2 + \beta_2^2\\
\end{split} s 1 ( 0 ) s 1 ( β 0 ) s 1 ( β 1 ) s 1 ( β 0 + β 1 ) s 1 ( β 2 ) s 1 ( β 0 + β 2 ) s 1 ( β 1 + β 2 ) s 1 ( β 0 + β 1 + β 2 ) = 0 = 0 = β 0 β 1 + β 1 2 = β 0 β 1 + β 1 2 = β 0 β 2 + β 2 2 = β 0 β 2 + β 2 2 = β 0 β 1 + β 1 2 + β 0 β 2 + β 2 2 = β 0 β 1 + β 1 2 + β 0 β 2 + β 2 2 上面的等式显示 s 1 ( V 3 ) s_1(V_3) s 1 ( V 3 ) V 3 V_3 V 3 V 2 V_2 V 2 V 2 = ⟨ β 0 ′ , β 1 ′ ⟩ = ⟨ β 0 β 1 + β 1 2 , β 0 β 2 + β 2 2 ⟩ V_2= \langle \beta'_0, \beta'_1\rangle = \langle \beta_0\beta_1 + \beta_1^2, \beta_0\beta_2 + \beta_2^2 \rangle V 2 = ⟨ β 0 ′ , β 1 ′ ⟩ = ⟨ β 0 β 1 + β 1 2 , β 0 β 2 + β 2 2 ⟩
这不是巧合,根据群同构定理,同态映射 ϕ : H → G \phi: H \to G ϕ : H → G G G G G ≅ H / K e r ( ϕ ) G\cong H/Ker(\phi) G ≅ H / Ker ( ϕ ) G G G ∣ G ∣ = ∣ H ∣ / ∣ K e r ( ϕ ) ∣ |G| = |H|/|Ker(\phi)| ∣ G ∣ = ∣ H ∣/∣ Ker ( ϕ ) ∣ s 1 : V 3 → V 2 s_1: V_3\to V_2 s 1 : V 3 → V 2 V 1 = K e r ( s 1 ) V_1=Ker(s_1) V 1 = Ker ( s 1 )
映射构成的链 ¶ 对于 V 2 = s 1 ( V 3 ) V_2 = s_1(V_3) V 2 = s 1 ( V 3 )
s 1 ′ ( X ) = X ⋅ ( X + β 0 β 1 + β 1 2 ) s_1'(X) = X\cdot (X+\beta_0\beta_1 + \beta_1^2) s 1 ′ ( X ) = X ⋅ ( X + β 0 β 1 + β 1 2 ) 可以继续将 V 2 V_2 V 2 V 1 = ⟨ β ′ ′ ⟩ V_1=\langle \beta''\rangle V 1 = ⟨ β ′′ ⟩ s 1 ( β 0 ′ ) s_1(\beta'_0) s 1 ( β 0 ′ ) s 1 ( β 1 ′ ) s_1(\beta'_1) s 1 ( β 1 ′ ) V 2 V_2 V 2
s 1 ′ ( β 0 β 1 + β 1 2 ) = 0 s 1 ′ ( β 0 β 1 + β 1 2 + β 0 β 2 + β 2 2 ) = β 0 2 β 1 β 2 + β 0 β 1 2 β 2 + β 0 2 β 2 2 + β 0 β 1 β 2 2 + β 1 2 β 2 2 + β 2 4 = β ′ ′ \begin{split}
s_1'(\beta_0\beta_1 + \beta_1^2) &= 0 \\
s_1'(\beta_0\beta_1 + \beta_1^2 + \beta_0\beta_2 + \beta_2^2)& = \beta_0^2\beta_1\beta_2 + \beta_0\beta_1^2\beta_2 + \beta_0^2\beta_2^2 + \beta_0\beta_1\beta_2^2 + \beta_1^2\beta_2^2 + \beta_2^4 \\
& = \beta''
\end{split} s 1 ′ ( β 0 β 1 + β 1 2 ) s 1 ′ ( β 0 β 1 + β 1 2 + β 0 β 2 + β 2 2 ) = 0 = β 0 2 β 1 β 2 + β 0 β 1 2 β 2 + β 0 2 β 2 2 + β 0 β 1 β 2 2 + β 1 2 β 2 2 + β 2 4 = β ′′ 其中 V 2 V_2 V 2 ( β 0 ′ , β 1 ′ ) (\beta'_0, \beta'_1) ( β 0 ′ , β 1 ′ ) β ′ ′ \beta'' β ′′
至此,我们得到一个映射的链:
V 3 ⟶ s 1 V 2 ⟶ s 1 ′ V 1 V_3 \overset{s_1}{\longrightarrow} V_2 \overset{s'_1}{\longrightarrow} V_1 V 3 ⟶ s 1 V 2 ⟶ s 1 ′ V 1 或者也可以写为:
⟨ β 0 , β 1 , β 2 ⟩ ⟶ s 1 ⟨ s 1 ( β 1 ) , s 1 ( β 2 ) ⟩ ⟶ s 1 ′ ⟨ s 1 ′ ( s 1 ( β 2 ) ) ⟩ \langle \beta_0, \beta_1, \beta_2 \rangle \overset{s_1}{\longrightarrow} \langle s_1(\beta_1), s_1(\beta_2) \rangle
\overset{s'_1}{\longrightarrow} \langle s'_1(s_1(\beta_2)) \rangle ⟨ β 0 , β 1 , β 2 ⟩ ⟶ s 1 ⟨ s 1 ( β 1 ) , s 1 ( β 2 )⟩ ⟶ s 1 ′ ⟨ s 1 ′ ( s 1 ( β 2 ))⟩ 并且每次映射到的线性子空间的维度都减一,即集合大小减半。这个代数结构是我们后续构造 FFT 与 FRI 协议的关键。
不难证明,对于任意的线性子空间,只要我们选定一个 Basis 之后,就可以依次构造 Degree 为 2 的 Subspace Polynomial 作为映射函数,然后通过映射得到一个维度减 1 的子空间,然后不断重复,直到子空间降至 1 维。当然 Basis 选择不同,以及 Subspace Polynomial 的选择不同都会导致不同的映射链。选择恰当的映射链可以显著提高计算的效率。
s 1 {s}_1 s 1 ¶ 我们定义映射链的初始子空间为 S ( 0 ) S^{(0)} S ( 0 ) S ( 1 ) S^{(1)} S ( 1 ) i i i S ( i ) S^{(i)} S ( i )
S ( 0 ) ⟶ s 1 S ( 1 ) ⟶ s 1 ( 1 ) ⋯ ⟶ s 1 ( n − 1 ) S ( n ) S^{(0)} \overset{s_1}{\longrightarrow} S^{(1)} \overset{s^{(1)}_1}{\longrightarrow} \cdots \overset{s^{(n-1)}_1}{\longrightarrow} S^{(n)} S ( 0 ) ⟶ s 1 S ( 1 ) ⟶ s 1 ( 1 ) ⋯ ⟶ s 1 ( n − 1 ) S ( n ) 给定 S ( i ) S^{(i)} S ( i ) B ( i ) = ( β 0 ( i ) , β 1 ( i ) , … , β s ( i ) ) B^{(i)}=(\beta^{(i)}_0, \beta^{(i)}_1,\ldots, \beta^{(i)}_s) B ( i ) = ( β 0 ( i ) , β 1 ( i ) , … , β s ( i ) ) s 1 ( i ) {s}^{(i)}_1 s 1 ( i ) S ( i ) S^{(i)} S ( i ) S ( i + 1 ) S^{(i+1)} S ( i + 1 ) S ( i + 1 ) S^{(i+1)} S ( i + 1 ) S ( i ) S^{(i)} S ( i ) s 1 ( i ) {s}^{(i)}_1 s 1 ( i ) s i ( i + 1 ) ( X ) {s}^{(i+1)}_i(X) s i ( i + 1 ) ( X )
我们假设 S ( 0 ) = ⟨ β 0 , β 1 , … , β k − 1 ⟩ S^{(0)}=\langle \beta_0, \beta_1, \ldots, \beta_{k-1}\rangle S ( 0 ) = ⟨ β 0 , β 1 , … , β k − 1 ⟩ B k B_k B k s 1 {s}_1 s 1 S ( 1 ) S^{(1)} S ( 1 ) B ( 1 ) B^{(1)} B ( 1 )
B ( 1 ) = ⟨ s 1 ( β 1 ) , s 1 ( β 2 ) , … , s 1 ( β k − 1 ) ⟩ B^{(1)} = \langle {\color{blue}{s}_1(\beta_1)}, {\color{blue}{s}_1(\beta_2)}, \ldots, {s}_1(\beta_{k-1}) \rangle B ( 1 ) = ⟨ s 1 ( β 1 ) , s 1 ( β 2 ) , … , s 1 ( β k − 1 )⟩ 在 S ( 1 ) S^{(1)} S ( 1 ) s 1 ( 1 ) ( X ) {s}^{(1)}_1(X) s 1 ( 1 ) ( X )
s 1 ( 1 ) ( X ) = X ( X + s 1 ( β 1 ) ) {s}^{(1)}_1(X) = {X(X+{s}_1(\beta_1))} s 1 ( 1 ) ( X ) = X ( X + s 1 ( β 1 )) 那么,S ( 1 ) S^{(1)} S ( 1 ) S ( 2 ) S^{(2)} S ( 2 ) S ( 0 ) S^{(0)} S ( 0 ) a ∈ S ( 0 ) a \in S^{(0)} a ∈ S ( 0 ) s 1 {s}_1 s 1 S ( 1 ) S^{(1)} S ( 1 ) s 1 ( 1 ) {s}^{(1)}_1 s 1 ( 1 ) S ( 2 ) S^{(2)} S ( 2 ) s 1 ( 1 ) ( s 1 ( X ) ) {s}^{(1)}_1({s}_1(X)) s 1 ( 1 ) ( s 1 ( X ))
s 1 ( 1 ) ( s 1 ( X ) ) = s 1 ( X ) ( s 1 ( X ) + s 1 ( β 1 ) ) = s 1 ( X ) ( s 1 ( X + β 1 ) ) ( additive homomorphism ) = s 2 ( X ) ( recurrency ) \begin{align*}
{s}^{(1)}_1({s}_1(X)) &= {s}_1(X)({s}_1(X)+{s}_1(\beta_1))
& \\[3ex]
&= {s}_1(X)({s}_1(X+\beta_1)) & (\text{additive homomorphism })\\[3ex]
&= {s}_2(X) & (\text{recurrency } )
\end{align*} s 1 ( 1 ) ( s 1 ( X )) = s 1 ( X ) ( s 1 ( X ) + s 1 ( β 1 )) = s 1 ( X ) ( s 1 ( X + β 1 )) = s 2 ( X ) ( additive homomorphism ) ( recurrency ) 于是我们推导出了 s 1 ( 1 ) ( s 1 ( X ) ) = s 2 ( X ) {s}^{(1)}_1({s}_1(X))={s}_2(X) s 1 ( 1 ) ( s 1 ( X )) = s 2 ( X ) s 2 {s}_2 s 2
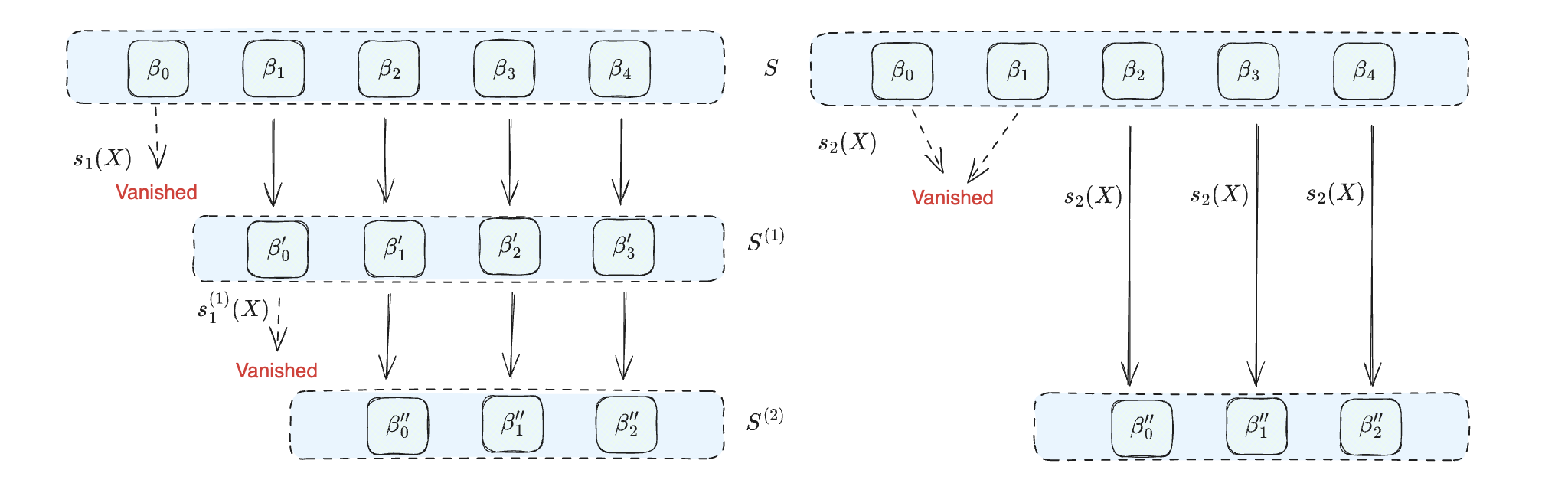
s 2 : S ( 0 ) → S ( 2 ) X ↦ X ( X + β 0 ) ( X + β 1 ) ( X + β 1 + β 0 ) \begin{split}
{s}_2: &S^{(0)} \to S^{(2)} \\[3ex]
& X \mapsto {X(X+\beta_0)(X+\beta_1)(X+\beta_1+\beta_0)} \\
\end{split} s 2 : S ( 0 ) → S ( 2 ) X ↦ X ( X + β 0 ) ( X + β 1 ) ( X + β 1 + β 0 ) 如下图所示,左右两种映射方式都会得到 S ( 2 ) S^{(2)} S ( 2 )
同理,我们可以得到下面的结论,对于折叠 j j j S ( j ) S^{(j)} S ( j )
S ( j ) = ⟨ s j ( β j ) , s j ( β j + 1 ) , … , s j ( β k − 1 ) ⟩ S^{(j)} = \langle {s}_{j}(\beta_j), {s}_{j}(\beta_{j+1}), \ldots, {s}_{j}(\beta_{k-1}) \rangle S ( j ) = ⟨ s j ( β j ) , s j ( β j + 1 ) , … , s j ( β k − 1 )⟩ 并且 s j {s}_{j} s j
s j ( X ) = s j − 1 ( 1 ) ( s 1 ( X ) ) = s j − 1 ( 1 ) ∘ s 1 s_{j}(X) = s^{(1)}_{j-1}(s_1(X)) = s^{(1)}_{j-1}\circ s_1 s j ( X ) = s j − 1 ( 1 ) ( s 1 ( X )) = s j − 1 ( 1 ) ∘ s 1 这个复合映射的等式可以解读为:先做一次 s 1 s_1 s 1 S ( 1 ) S^{(1)} S ( 1 ) j − 1 j-1 j − 1 s j − 1 ( 1 ) s^{(1)}_{j-1} s j − 1 ( 1 ) j j j s j s_{j} s j S ( j ) S^{(j)} S ( j )
同样,我们还能证明:如果先做一次 j − 1 j-1 j − 1 s j − 1 s_{j-1} s j − 1 S ( j − 1 ) S^{(j-1)} S ( j − 1 ) S ( j ) S^{(j)} S ( j )
s j ( X ) = s 1 ( 1 ) ( s j − 1 ( X ) ) = s 1 ( 1 ) ∘ s j − 1 s_{j}(X) = s^{(1)}_{1}(s_{j-1}(X)) = s^{(1)}_{1}\circ s_{j-1} s j ( X ) = s 1 ( 1 ) ( s j − 1 ( X )) = s 1 ( 1 ) ∘ s j − 1 更一般地,我们可以证明得到下面的重要性质,即在任意子空间 S ( i ) S^{(i)} S ( i ) j j j j j j
s j ( i ) ( X ) = s 1 ( i + j − 1 ) ∘ s 1 ( i + j − 2 ) ∘ ⋯ ∘ s 1 ( i ) s^{(i)}_{j}(X) = s^{(i+j-1)}_1\circ s^{(i+j-2)}_1\circ \cdots \circ s^{(i)}_1 s j ( i ) ( X ) = s 1 ( i + j − 1 ) ∘ s 1 ( i + j − 2 ) ∘ ⋯ ∘ s 1 ( i ) 多项式的 Polynomial Basis ¶ 对于一个次数小于 N = 2 n N=2^n N = 2 n f ( X ) ∈ F [ X ] < N f(X) \in \mathbb{F}[X]^{<N} f ( X ) ∈ F [ X ] < N
f ( X ) = c 0 + c 1 X + c 2 X 2 + … + c N − 1 X N − 1 f(X) = c_0 + c_1X + c_2X^2 + \ldots + c_{N-1}X^{N-1} f ( X ) = c 0 + c 1 X + c 2 X 2 + … + c N − 1 X N − 1 其中 c ⃗ = ( c 0 , c 1 , … , c N − 1 ) \vec{c}=(c_0, c_1, \ldots, c_{N-1}) c = ( c 0 , c 1 , … , c N − 1 ) ( 1 , X , X 2 , … , X N − 1 ) (1, X, X^2, \ldots, X^{N-1}) ( 1 , X , X 2 , … , X N − 1 ) B m o n o \mathcal{B}^{mono} B m o n o
B m o n o = ( 1 , X , X 2 , … , X N − 1 ) \mathcal{B}^{mono}=(1, X, X^2, \ldots, X^{N-1}) B m o n o = ( 1 , X , X 2 , … , X N − 1 ) 这个基向量也可以表达为下面的 Tensor Product 形式:
B m o n o = ( 1 , X ) ⊗ ( 1 , X 2 ) ⊗ … ⊗ ( 1 , X 2 n − 1 ) \mathcal{B}^{mono}=(1, X) \otimes (1, X^2) \otimes \ldots \otimes (1, X^{2^{n-1}}) B m o n o = ( 1 , X ) ⊗ ( 1 , X 2 ) ⊗ … ⊗ ( 1 , X 2 n − 1 ) 一元多项式的 「点值式」称为 Lagrange Basis 表示。即我们可以用 N N N
通过多项式除法,我们可以得到多项式在 B m o n o \mathcal{B}^{mono} B m o n o t ( X ) t(X) t ( X ) X 4 ⋅ X 2 ⋅ X X^4\cdot X^2\cdot X X 4 ⋅ X 2 ⋅ X t ( X ) / ( X 4 ⋅ X 2 ⋅ X ) t(X)/(X^4\cdot X^2\cdot X) t ( X ) / ( X 4 ⋅ X 2 ⋅ X ) c 7 c_7 c 7 t ′ ( X ) t'(X) t ′ ( X ) t ′ ( X ) / ( X 4 ⋅ X 2 ) t'(X)/(X^4\cdot X^2) t ′ ( X ) / ( X 4 ⋅ X 2 ) B 6 m o n o = X 6 \mathcal{B}^{mono}_6 = X^6 B 6 m o n o = X 6 c 6 c_6 c 6 t ( X ) t(X) t ( X ) B m o n o \mathcal{B}^{mono} B m o n o c ⃗ = ( c 0 , c 1 , … , c 7 ) \vec{c}=(c_0, c_1, \ldots, c_7) c = ( c 0 , c 1 , … , c 7 )
t ( X ) = c 0 + c 1 X + c 2 X 2 + … + c 7 X 7 t(X) = c_0 + c_1X + c_2X^2 + \ldots + c_7X^7 t ( X ) = c 0 + c 1 X + c 2 X 2 + … + c 7 X 7 利用前文已讨论过的 Subspace Polynomial s k ( X ) s_k(X) s k ( X ) s k ( X ) s_k(X) s k ( X ) 2 k 2^k 2 k ( 1 , X , X 2 , X 4 ) (1, X, X^2, X^4) ( 1 , X , X 2 , X 4 ) ( s 0 ( X ) , s 1 ( X ) , s 2 ( X ) ) (s_0(X), s_1(X), s_2(X)) ( s 0 ( X ) , s 1 ( X ) , s 2 ( X )) B m o n o \mathcal{B}^{mono} B m o n o B n o v e l \mathcal{B}^{novel} B n o v e l
B n o v e l = ( 1 , s 0 ( X ) ) ⊗ ( 1 , s 1 ( X ) ) ⊗ … ⊗ ( 1 , s n − 1 ( X ) ) \mathcal{B}^{novel} = (1, s_0(X)) \otimes (1, s_1(X)) \otimes \ldots \otimes (1, s_{n-1}(X)) B n o v e l = ( 1 , s 0 ( X )) ⊗ ( 1 , s 1 ( X )) ⊗ … ⊗ ( 1 , s n − 1 ( X )) 请注意与论文 [LCH14] 和 [DP24] 不同的是,这里我们暂时没有引入 Normalized Subspace Polynomial,以方便大家理解。回到上面的定义,其中每一个分量 B i n o v e l \mathcal{B}^{novel}_i B i n o v e l X i ( X ) \mathcal{X}_i(X) X i ( X )
X i ( X ) = ∏ j = 0 n − 1 ( s j ( X ) ) i j , where b i t s ( i ) = ( i 0 , i 1 , … , i n − 1 ) \mathcal{X}_i(X) = \prod_{j=0}^{n-1}(s_j(X))^{i_j}, \text{ where $\mathsf{bits}(i)=(i_0, i_1, \ldots, i_{n-1})$} X i ( X ) = j = 0 ∏ n − 1 ( s j ( X ) ) i j , where bits ( i ) = ( i 0 , i 1 , … , i n − 1 ) 这里 b i t s ( i ) \mathsf{bits}(i) bits ( i ) i i i i = 5 i=5 i = 5 b i t s ( 5 ) = ( 1 , 0 , 1 ) \mathsf{bits}(5)=(1, 0, 1) bits ( 5 ) = ( 1 , 0 , 1 ) b i t s ( 6 ) = ( 0 , 1 , 1 ) \mathsf{bits}(6) = (0, 1, 1) bits ( 6 ) = ( 0 , 1 , 1 ) n = 3 , N = 8 n=3, N=8 n = 3 , N = 8 ( X 0 ( X ) , X 1 ( X ) , … , X 7 ( X ) ) \big(\mathcal{X}_0(X), \mathcal{X}_1(X),\ldots, \mathcal{X}_7(X)\big) ( X 0 ( X ) , X 1 ( X ) , … , X 7 ( X ) )
X 0 ( X ) = 1 X 1 ( X ) = s 0 ( X ) = X X 2 ( X ) = s 1 ( X ) X 3 ( X ) = s 0 ( X ) ⋅ s 1 ( X ) X 4 ( X ) = s 2 ( X ) X 5 ( X ) = s 0 ( X ) ⋅ s 2 ( X ) X 6 ( X ) = s 1 ( X ) ⋅ s 2 ( X ) X 7 ( X ) = s 0 ( X ) ⋅ s 1 ( X ) ⋅ s 2 ( X ) \begin{split}
\mathcal{X}_0(X) &= 1 \\
\mathcal{X}_1(X) &= s_0(X) = X\\
\mathcal{X}_2(X) &= s_1(X) \\
\mathcal{X}_3(X) &= s_0(X)\cdot s_1(X)\\
\mathcal{X}_4(X) &= s_2(X)\\
\mathcal{X}_5(X) &= s_0(X)\cdot s_2(X)\\
\mathcal{X}_6(X) &= s_1(X)\cdot s_2(X) \\
\mathcal{X}_7(X) &= s_0(X)\cdot s_1(X)\cdot s_2(X) \\
\end{split} X 0 ( X ) X 1 ( X ) X 2 ( X ) X 3 ( X ) X 4 ( X ) X 5 ( X ) X 6 ( X ) X 7 ( X ) = 1 = s 0 ( X ) = X = s 1 ( X ) = s 0 ( X ) ⋅ s 1 ( X ) = s 2 ( X ) = s 0 ( X ) ⋅ s 2 ( X ) = s 1 ( X ) ⋅ s 2 ( X ) = s 0 ( X ) ⋅ s 1 ( X ) ⋅ s 2 ( X ) 容易检验,每一个 Basis 分量 X i ( X ) \mathcal{X}_i(X) X i ( X ) i i i B n o v e l \mathcal{B}^{novel} B n o v e l f ( X ) ∈ F 2 m [ X ] f(X)\in \mathbb{F}_{2^m}[X] f ( X ) ∈ F 2 m [ X ]
f ( X ) = a 0 X 0 ( X ) + a 1 X 1 ( X ) + … + a 7 X 7 ( X ) = a 0 + a 1 s 0 ( X ) + a 2 s 1 ( X ) + a 3 s 0 ( X ) ⋅ s 1 ( X ) + a 4 s 2 ( X ) + a 5 s 0 ( X ) ⋅ s 2 ( X ) + a 6 s 1 ( X ) ⋅ s 2 ( X ) + a 7 s 0 ( X ) ⋅ s 1 ( X ) ⋅ s 2 ( X ) \begin{split}
f(X) &= a_0\mathcal{X}_0(X) + a_1\mathcal{X}_1(X) + \ldots + a_7\mathcal{X}_7(X)\\
&= a_0 + a_1s_0(X) + a_2s_1(X) + a_3s_0(X)\cdot {s}_1(X) \\
& + a_4s_2(X) + a_5{s}_0(X)\cdot {s}_2(X) + a_6{s}_1(X)\cdot {s}_2(X) + a_7{s}_0(X)\cdot {s}_1(X)\cdot s_2(X) \\
\end{split} f ( X ) = a 0 X 0 ( X ) + a 1 X 1 ( X ) + … + a 7 X 7 ( X ) = a 0 + a 1 s 0 ( X ) + a 2 s 1 ( X ) + a 3 s 0 ( X ) ⋅ s 1 ( X ) + a 4 s 2 ( X ) + a 5 s 0 ( X ) ⋅ s 2 ( X ) + a 6 s 1 ( X ) ⋅ s 2 ( X ) + a 7 s 0 ( X ) ⋅ s 1 ( X ) ⋅ s 2 ( X ) 同样,我们可以利用多项式除法来将一个多项式在 B n o v e l \mathcal{B}^{novel} B n o v e l B m o n o \mathcal{B}^{mono} B m o n o
Additive FFT ¶ 类似 Multiplicative FFT,要构造 Additive FFT,我们需要在 F 2 m \mathbb{F}_{2^m} F 2 m
S ( 0 ) ⟶ s 1 S ( 1 ) ⟶ s 1 ( 1 ) ⋯ ⟶ s 1 ( n − 1 ) S ( n ) S^{(0)} \overset{s_1}{\longrightarrow} S^{(1)} \overset{s^{(1)}_1}{\longrightarrow} \cdots \overset{s^{(n-1)}_1}{\longrightarrow} S^{(n)} S ( 0 ) ⟶ s 1 S ( 1 ) ⟶ s 1 ( 1 ) ⋯ ⟶ s 1 ( n − 1 ) S ( n ) 为了演示方便,指定 n = 3 n=3 n = 3 S ( 0 ) = ⟨ β 0 , β 1 , β 2 ⟩ S^{(0)}=\langle \beta_0, \beta_1, \beta_2\rangle S ( 0 ) = ⟨ β 0 , β 1 , β 2 ⟩ B n o v e l \mathcal{B}^{novel} B n o v e l f ( X ) f(X) f ( X )
f ( X ) = a 0 X 0 ( X ) + a 1 X 1 ( X ) + … + a 7 X 7 ( X ) = a 0 + a 1 s 0 ( X ) + a 2 s 1 ( X ) + a 3 s 0 ( X ) ⋅ s 1 ( X ) + a 4 s 2 ( X ) + a 5 s 0 ( X ) ⋅ s 2 ( X ) + a 6 s 1 ( X ) ⋅ s 2 ( X ) + a 7 s 0 ( X ) ⋅ s 1 ( X ) ⋅ s 2 ( X ) = ( a 0 + a 2 s 1 ( X ) + a 4 s 2 ( X ) + a 6 s 1 ( X ) ⋅ s 2 ( X ) ) + ( a 1 + a 3 s 0 ( X ) ⋅ s 1 ( X ) + a 5 s 0 ( X ) ⋅ s 2 ( X ) + a 7 s 0 ( X ) ⋅ s 1 ( X ) ⋅ s 2 ( X ) ) = ( a 0 + a 2 s 1 ( X ) + a 4 s 2 ( X ) + a 6 s 1 ( X ) ⋅ s 2 ( X ) ) + s 0 ( X ) ⋅ ( a 1 + a 3 ⋅ s 1 ( X ) + a 5 ⋅ s 2 ( X ) + a 7 ⋅ s 1 ( X ) ⋅ s 2 ( X ) ) \begin{split}
f(X) &= a_0\mathcal{X}_0(X) + a_1\mathcal{X}_1(X) + \ldots + a_7\mathcal{X}_7(X)\\
&= a_0 + a_1{s}_0(X) + a_2{s}_1(X) + a_3{s}_0(X)\cdot {s}_1(X) \\
& \qquad + a_4{s}_2(X) + a_5{s}_0(X)\cdot {s}_2(X) + a_6{s}_1(X)\cdot {s}_2(X) + a_7{s}_0(X)\cdot {s}_1(X)\cdot {s}_2(X) \\
& = \big(a_0 + a_2 {s}_1(X) + a_4{s}_2(X) + a_6{s}_1(X)\cdot {s}_2(X)\big) \\
& \qquad + \big(a_1 + a_3{s}_0(X)\cdot {s}_1(X) + a_5{s}_0(X)\cdot{s}_2(X) + a_7{s}_0(X)\cdot{s}_1(X)\cdot {s}_2(X)\big) \\
& = \big(a_0 + a_2 {s}_1(X) + a_4{s}_2(X) + a_6{s}_1(X)\cdot {s}_2(X)\big) \\
& \qquad + {\color{red}{s}_0(X)}\cdot \big(a_1 + a_3\cdot{s}_1(X) + a_5\cdot{s}_2(X) + a_7\cdot{s}_1(X)\cdot {s}_2(X)\big) \\
\end{split} f ( X ) = a 0 X 0 ( X ) + a 1 X 1 ( X ) + … + a 7 X 7 ( X ) = a 0 + a 1 s 0 ( X ) + a 2 s 1 ( X ) + a 3 s 0 ( X ) ⋅ s 1 ( X ) + a 4 s 2 ( X ) + a 5 s 0 ( X ) ⋅ s 2 ( X ) + a 6 s 1 ( X ) ⋅ s 2 ( X ) + a 7 s 0 ( X ) ⋅ s 1 ( X ) ⋅ s 2 ( X ) = ( a 0 + a 2 s 1 ( X ) + a 4 s 2 ( X ) + a 6 s 1 ( X ) ⋅ s 2 ( X ) ) + ( a 1 + a 3 s 0 ( X ) ⋅ s 1 ( X ) + a 5 s 0 ( X ) ⋅ s 2 ( X ) + a 7 s 0 ( X ) ⋅ s 1 ( X ) ⋅ s 2 ( X ) ) = ( a 0 + a 2 s 1 ( X ) + a 4 s 2 ( X ) + a 6 s 1 ( X ) ⋅ s 2 ( X ) ) + s 0 ( X ) ⋅ ( a 1 + a 3 ⋅ s 1 ( X ) + a 5 ⋅ s 2 ( X ) + a 7 ⋅ s 1 ( X ) ⋅ s 2 ( X ) ) 然后我们引入两个辅助多项式 f e v e n ( X ) , f o d d ( X ) f_{even}(X), f_{odd}(X) f e v e n ( X ) , f o dd ( X )
f e v e n ( X ) = a 0 + a 2 ⋅ s 1 ( X ) + a 4 ⋅ s 2 ( X ) + a 6 ⋅ s 1 ( X ) ⋅ s 2 ( X ) f o d d ( X ) = a 1 + a 3 ⋅ s 1 ( X ) + a 5 ⋅ s 2 ( X ) + a 7 ⋅ s 1 ( X ) ⋅ s 2 ( X ) \begin{split}
f_{even}(X) &= a_0 + a_2\cdot {s}_1(X) + a_4\cdot {s}_2(X) + a_6\cdot {s}_1(X)\cdot {s}_2(X) \\
f_{odd}(X) &= a_1 + a_3\cdot{s}_1(X) + a_5\cdot{s}_2(X) + a_7\cdot{s}_1(X)\cdot {s}_2(X) \\
\end{split} f e v e n ( X ) f o dd ( X ) = a 0 + a 2 ⋅ s 1 ( X ) + a 4 ⋅ s 2 ( X ) + a 6 ⋅ s 1 ( X ) ⋅ s 2 ( X ) = a 1 + a 3 ⋅ s 1 ( X ) + a 5 ⋅ s 2 ( X ) + a 7 ⋅ s 1 ( X ) ⋅ s 2 ( X ) 根据我们之前推导的映射的复合性质,s 1 ( X ) = s 0 ( 1 ) ∘ s 1 ( X ) s_1(X)=s^{(1)}_0\circ s_1(X) s 1 ( X ) = s 0 ( 1 ) ∘ s 1 ( X ) s 2 ( X ) = s 1 ( 1 ) ∘ s 1 ( X ) s_2(X)=s^{(1)}_1\circ s_1(X) s 2 ( X ) = s 1 ( 1 ) ∘ s 1 ( X )
f e v e n ( X ) = a 0 + a 2 ⋅ s 0 ( 1 ) ( s 1 ( X ) ) + a 4 ⋅ s 1 ( 1 ) ( s 1 ( X ) ) + a 6 ⋅ s 0 ( 1 ) ( s 1 ( X ) ) ⋅ s 1 ( 1 ) ( s 1 ( X ) ) = a 0 + a 2 ⋅ s 0 ( 1 ) ( s 1 ( X ) ) + a 4 ⋅ s 1 ( 1 ) ( s 1 ( X ) ) + a 6 ⋅ s 0 ( 1 ) ( s 1 ( X ) ) ⋅ s 1 ( 1 ) ( s 1 ( X ) ) f o d d ( X ) = a 1 + a 3 ⋅ s 0 ( 1 ) ( s 1 ( X ) ) + a 5 ⋅ s 1 ( 1 ) ( s 1 ( X ) ) + a 7 ⋅ s 0 ( 1 ) ( s 1 ( X ) ) ⋅ s 1 ( 1 ) ( s 1 ( X ) ) = a 1 + a 3 ⋅ s 0 ( 1 ) ( s 1 ( X ) ) + a 5 ⋅ s 1 ( 1 ) ( s 1 ( X ) ) + a 7 ⋅ s 0 ( 1 ) ( s 1 ( X ) ) ⋅ s 1 ( 1 ) ( s 1 ( X ) ) \begin{split}
f_{even}(X) &= a_0 + a_2 \cdot s^{(1)}_0(s_1(X)) + a_4 \cdot s^{(1)}_1(s_1(X)) + a_6 \cdot s^{(1)}_0(s_1(X))\cdot s^{(1)}_1(s_1(X)) \\
& = a_0 + a_2 \cdot s^{(1)}_0({\color{blue}s_1(X)}) + a_4 \cdot s^{(1)}_1({\color{blue}s_1(X)}) + a_6 \cdot s^{(1)}_0({\color{blue}s_1(X)})\cdot s^{(1)}_1({\color{blue}s_1(X)}) \\
f_{odd}(X) &= a_1 + a_3 \cdot s^{(1)}_0(s_1(X)) + a_5 \cdot s^{(1)}_1(s_1(X)) + a_7 \cdot s^{(1)}_0(s_1(X))\cdot s^{(1)}_1(s_1(X)) \\
& = a_1 + a_3 \cdot s^{(1)}_0({\color{blue}s_1(X)}) + a_5 \cdot s^{(1)}_1({\color{blue}s_1(X)}) + a_7 \cdot s^{(1)}_0({\color{blue}s_1(X)})\cdot s^{(1)}_1({\color{blue}s_1(X)}) \\
\end{split} f e v e n ( X ) f o dd ( X ) = a 0 + a 2 ⋅ s 0 ( 1 ) ( s 1 ( X )) + a 4 ⋅ s 1 ( 1 ) ( s 1 ( X )) + a 6 ⋅ s 0 ( 1 ) ( s 1 ( X )) ⋅ s 1 ( 1 ) ( s 1 ( X )) = a 0 + a 2 ⋅ s 0 ( 1 ) ( s 1 ( X ) ) + a 4 ⋅ s 1 ( 1 ) ( s 1 ( X ) ) + a 6 ⋅ s 0 ( 1 ) ( s 1 ( X ) ) ⋅ s 1 ( 1 ) ( s 1 ( X ) ) = a 1 + a 3 ⋅ s 0 ( 1 ) ( s 1 ( X )) + a 5 ⋅ s 1 ( 1 ) ( s 1 ( X )) + a 7 ⋅ s 0 ( 1 ) ( s 1 ( X )) ⋅ s 1 ( 1 ) ( s 1 ( X )) = a 1 + a 3 ⋅ s 0 ( 1 ) ( s 1 ( X ) ) + a 5 ⋅ s 1 ( 1 ) ( s 1 ( X ) ) + a 7 ⋅ s 0 ( 1 ) ( s 1 ( X ) ) ⋅ s 1 ( 1 ) ( s 1 ( X ) ) 代入 Y = s 1 ( X ) {\color{blue}Y=s_1(X)} Y = s 1 ( X ) f ( X ) f(X) f ( X ) f e v e n ( Y ) f_{even}({\color{blue}Y}) f e v e n ( Y ) f o d d ( Y ) f_{odd}({\color{blue}Y}) f o dd ( Y )
f ( X ) = f e v e n ( Y ) + s 0 ( X ) ⋅ f o d d ( Y ) \begin{split}
f(X) & = f_{even}({\color{blue}Y}) + {s}_0(X)\cdot f_{odd}({\color{blue}Y})
\end{split} f ( X ) = f e v e n ( Y ) + s 0 ( X ) ⋅ f o dd ( Y ) 而多项式 f e v e n ( Y ) f_{even}({\color{blue}Y}) f e v e n ( Y ) f o d d ( Y ) f_{odd}({\color{blue}Y}) f o dd ( Y ) X ( 1 ) \mathcal{X}^{(1)} X ( 1 )
X 0 ( 1 ) ( X ) = 1 X 1 ( 1 ) ( X ) = s 0 ( 1 ) ( X ) = s 0 ( s 1 ( X ) ) = s 1 ( X ) X 2 ( 1 ) ( X ) = s 1 ( 1 ) ( X ) = s 1 ( s 1 ( X ) ) = s 2 ( X ) X 3 ( 1 ) ( X ) = s 0 ( 1 ) ( X ) ⋅ s 1 ( 1 ) ( X ) = s 0 ( s 1 ( X ) ) ⋅ s 1 ( s 1 ( X ) ) = s 1 ( X ) ⋅ s 2 ( X ) \begin{array}{llll}
\mathcal{X}^{(1)}_0(X) &= 1 \\
\mathcal{X}^{(1)}_1(X) &= {s}^{(1)}_0(X) & = {s}_0({s}_1(X)) & = {s}_1(X) \\
\mathcal{X}^{(1)}_2(X) &= {s}^{(1)}_1(X) & = {s}_1({s}_1(X)) & = {s}_2(X) \\
\mathcal{X}^{(1)}_3(X) &= {s}^{(1)}_0(X)\cdot {s}^{(1)}_1(X) & = {s}_0({s}_1(X)) \cdot {s}_1({s}_1(X)) & = {s}_1(X) \cdot {s}_2(X)\\
\end{array} X 0 ( 1 ) ( X ) X 1 ( 1 ) ( X ) X 2 ( 1 ) ( X ) X 3 ( 1 ) ( X ) = 1 = s 0 ( 1 ) ( X ) = s 1 ( 1 ) ( X ) = s 0 ( 1 ) ( X ) ⋅ s 1 ( 1 ) ( X ) = s 0 ( s 1 ( X )) = s 1 ( s 1 ( X )) = s 0 ( s 1 ( X )) ⋅ s 1 ( s 1 ( X )) = s 1 ( X ) = s 2 ( X ) = s 1 ( X ) ⋅ s 2 ( X ) 重写下奇偶多项式:
f e v e n ( X ) = a 0 ⋅ X 0 ( 1 ) ( X ) + a 2 ⋅ X 1 ( 1 ) ( X ) + a 4 ⋅ X 2 ( 1 ) ( X ) + a 6 ⋅ X 3 ( 1 ) ( X ) f o d d ( X ) = a 1 ⋅ X 0 ( 1 ) ( X ) + a 3 ⋅ X 1 ( 1 ) ( X ) + a 5 ⋅ X 2 ( 1 ) ( X ) + a 7 ⋅ X 3 ( 1 ) ( X ) \begin{split}
f_{even}(X) &= a_0\cdot\mathcal{X}^{(1)}_0(X) + a_2\cdot \mathcal{X}^{(1)}_1(X) + a_4\cdot \mathcal{X}^{(1)}_2(X) + a_6\cdot \mathcal{X}^{(1)}_3(X) \\
f_{odd}(X) &= a_1\cdot\mathcal{X}^{(1)}_0(X) + a_3\cdot \mathcal{X}^{(1)}_1(X) + a_5\cdot \mathcal{X}^{(1)}_2(X) + a_7\cdot \mathcal{X}^{(1)}_3(X)
\end{split} f e v e n ( X ) f o dd ( X ) = a 0 ⋅ X 0 ( 1 ) ( X ) + a 2 ⋅ X 1 ( 1 ) ( X ) + a 4 ⋅ X 2 ( 1 ) ( X ) + a 6 ⋅ X 3 ( 1 ) ( X ) = a 1 ⋅ X 0 ( 1 ) ( X ) + a 3 ⋅ X 1 ( 1 ) ( X ) + a 5 ⋅ X 2 ( 1 ) ( X ) + a 7 ⋅ X 3 ( 1 ) ( X ) 从结构上看,这个等式与 Multiplicative FFT 中的 f ( X ) = f e v e n ( X 2 ) + X ⋅ f o d d ( X 2 ) f(X)=f_{even}(X^2) + X\cdot f_{odd}(X^2) f ( X ) = f e v e n ( X 2 ) + X ⋅ f o dd ( X 2 ) X ↦ X 2 X\mapsto X^2 X ↦ X 2 s 1 : X ↦ X ( X + β 0 ) s_1: X \mapsto X(X+\beta_0) s 1 : X ↦ X ( X + β 0 ) S ( 0 ) S^{(0)} S ( 0 ) s 1 s_1 s 1 S ( 1 ) S^{(1)} S ( 1 )
S ( 1 ) = ⟨ s 1 ( β 1 ) , s 1 ( β 2 ) ⟩ S^{(1)} = \langle s_1(\beta_1), s_1(\beta_2) \rangle S ( 1 ) = ⟨ s 1 ( β 1 ) , s 1 ( β 2 )⟩ 于是我们可以依赖递归调用,求得 { f e v e n ( X ) ∣ X ∈ S ( 1 ) } \{f_{even}(X) \mid X\in S^{(1)}\} { f e v e n ( X ) ∣ X ∈ S ( 1 ) } { f o d d ( X ) ∣ X ∈ S ( 1 ) } \{ f_{odd}(X) \mid X\in S^{(1)}\} { f o dd ( X ) ∣ X ∈ S ( 1 ) } f ( X ) = f e v e n ( X ) + s 0 ( X ) ⋅ f o d d ( X ) f(X)=f_{even}(X) + s_0(X)\cdot f_{odd}(X) f ( X ) = f e v e n ( X ) + s 0 ( X ) ⋅ f o dd ( X ) f ( X ) f(X) f ( X ) S ( 0 ) S^{(0)} S ( 0 )
下面我们假设递归调用成功返回,那么我们就得到了 f e v e n ( X ) f_{even}(X) f e v e n ( X ) f o d d ( X ) f_{odd}(X) f o dd ( X ) S ( 1 ) S^{(1)} S ( 1 ) u ⃗ \vec{u} u v ⃗ \vec{v} v
( u 0 , u 1 , u 2 , u 3 ) = ( f e v e n ( 0 ) , f e v e n ( 1 ) , f e v e n ( s 1 ( β 1 ) ) , f e v e n ( s 1 ( β 1 ) + 1 ) ) ( v 0 , v 1 , v 2 , v 3 ) = ( f o d d ( 0 ) , f o d d ( 1 ) , f o d d ( s 1 ( β 1 ) ) , f o d d ( s 1 ( β 1 ) + 1 ) ) \begin{split}
(u_0, u_1, u_2, u_3) &= \big(f_{even}(0), f_{even}(1), f_{even}(s_1(\beta_1)), f_{even}(s_1(\beta_1) + 1)\big)\\[2ex]
(v_0, v_1, v_2, v_3) &= \big(f_{odd}(0), f_{odd}(1), f_{odd}(s_1(\beta_1)), f_{odd}(s_1(\beta_1) + 1)\big)\\
\end{split} ( u 0 , u 1 , u 2 , u 3 ) ( v 0 , v 1 , v 2 , v 3 ) = ( f e v e n ( 0 ) , f e v e n ( 1 ) , f e v e n ( s 1 ( β 1 )) , f e v e n ( s 1 ( β 1 ) + 1 ) ) = ( f o dd ( 0 ) , f o dd ( 1 ) , f o dd ( s 1 ( β 1 )) , f o dd ( s 1 ( β 1 ) + 1 ) ) 然后我们就可以计算 f ( X ) f(X) f ( X ) S ( 0 ) S^{(0)} S ( 0 ) f ( X ) ∣ S ( 0 ) f(X)\mid_{S^{(0)}} f ( X ) ∣ S ( 0 )
f ( 0 ) = f e v e n ( s 1 ( 0 ) ) + 0 ⋅ f o d d ( s 1 ( 0 ) ) = u 0 f ( 1 ) = f e v e n ( s 1 ( 1 ) ) + 1 ⋅ v 1 = u 0 + v 1 f ( β 1 ) = f e v e n ( s 1 ( β 1 ) ) + β 1 ⋅ f o d d ( s 1 ( β 1 ) ) = u 1 + β 1 ⋅ v 1 f ( β 1 + 1 ) = f e v e n ( s 1 ( β 1 ) + s 1 ( 1 ) ) + ( β 1 + 1 ) ⋅ f o d d ( s 1 ( β 1 ) + s 1 ( 1 ) ) = u 1 + β 1 ⋅ v 1 + v 1 f ( β 2 ) = f e v e n ( s 1 ( β 2 ) ) + β 2 ⋅ f o d d ( s 1 ( β 2 ) ) = u 2 + β 2 ⋅ v 2 f ( β 2 + 1 ) = f e v e n ( s 1 ( β 2 ) + s 1 ( 1 ) ) + ( β 2 + 1 ) ⋅ f o d d ( s 1 ( β 2 ) + s 1 ( 1 ) ) = u 2 + β 2 ⋅ v 2 + v 2 f ( β 2 + β 1 ) = f e v e n ( s 1 ( β 2 ) + s 1 ( β 1 ) ) + ( β 2 + β 1 ) ⋅ f o d d ( s 1 ( β 2 ) + s 1 ( β 1 ) ) = u 3 + β 2 ⋅ v 3 + β 1 ⋅ v 3 f ( β 2 + β 1 + 1 ) = f e v e n ( s 1 ( β 2 ) + s 1 ( β 1 ) + s 1 ( 1 ) ) + ( β 2 + β 1 + 1 ) ⋅ f o d d ( s 1 ( β 2 ) + s 1 ( β 1 ) + s 1 ( 1 ) ) = u 3 + β 2 ⋅ v 3 + β 1 ⋅ v 3 + v 3 \begin{array}{rlll}
f(0) &= f_{even}({s}_1(0)) + 0\cdot f_{odd}({s}_1(0)) \\
& = u_0\\[1ex]
f(1) &= f_{even}({s}_1(1)) + 1\cdot v_1 \\
& = u_0 + v_1 \\[1ex]
f(\beta_1) &= f_{even}({s}_1(\beta_1)) + \beta_1\cdot f_{odd}({s}_1(\beta_1)) \\
& = u_1 + \beta_1 \cdot v_1\\[1ex]
f(\beta_1+1) &= f_{even}({s}_1(\beta_1)+{s}_1(1)) + (\beta_1 +1)\cdot f_{odd}({s}_1(\beta_1)+{s}_1(1)) \\
& = u_1 + \beta_1\cdot v_1 + v_1\\[1ex]
f(\beta_2) &= f_{even}({s}_1(\beta_2)) + \beta_2 \cdot f_{odd}({s}_1(\beta_2)) \\
& = u_2 + \beta_2\cdot v_2 \\[1ex]
f(\beta_2+1) &= f_{even}({s}_1(\beta_2)+{s}_1(1)) + (\beta_2 +1) \cdot f_{odd}({s}_1(\beta_2)+{s}_1(1)) \\
& = u_2 + \beta_2\cdot v_2 + v_2\\[1ex]
f(\beta_2+\beta_1) &= f_{even}({s}_1(\beta_2)+{s}_1(\beta_1)) + (\beta_2 + \beta_1) \cdot f_{odd}({s}_1(\beta_2)+{s}_1(\beta_1)) \\
& = u_3 + \beta_2\cdot v_3 + \beta_1\cdot v_3 \\[1ex]
f(\beta_2+\beta_1+1) &= f_{even}({s}_1(\beta_2)+{s}_1(\beta_1)+{s}_1(1)) + (\beta_2 + \beta_1 + 1) \cdot f_{odd}({s}_1(\beta_2)+{s}_1(\beta_1)+{s}_1(1)) \\
& = u_3 + \beta_2\cdot v_3 + \beta_1\cdot v_3 + v_3\\[1ex]
\end{array} f ( 0 ) f ( 1 ) f ( β 1 ) f ( β 1 + 1 ) f ( β 2 ) f ( β 2 + 1 ) f ( β 2 + β 1 ) f ( β 2 + β 1 + 1 ) = f e v e n ( s 1 ( 0 )) + 0 ⋅ f o dd ( s 1 ( 0 )) = u 0 = f e v e n ( s 1 ( 1 )) + 1 ⋅ v 1 = u 0 + v 1 = f e v e n ( s 1 ( β 1 )) + β 1 ⋅ f o dd ( s 1 ( β 1 )) = u 1 + β 1 ⋅ v 1 = f e v e n ( s 1 ( β 1 ) + s 1 ( 1 )) + ( β 1 + 1 ) ⋅ f o dd ( s 1 ( β 1 ) + s 1 ( 1 )) = u 1 + β 1 ⋅ v 1 + v 1 = f e v e n ( s 1 ( β 2 )) + β 2 ⋅ f o dd ( s 1 ( β 2 )) = u 2 + β 2 ⋅ v 2 = f e v e n ( s 1 ( β 2 ) + s 1 ( 1 )) + ( β 2 + 1 ) ⋅ f o dd ( s 1 ( β 2 ) + s 1 ( 1 )) = u 2 + β 2 ⋅ v 2 + v 2 = f e v e n ( s 1 ( β 2 ) + s 1 ( β 1 )) + ( β 2 + β 1 ) ⋅ f o dd ( s 1 ( β 2 ) + s 1 ( β 1 )) = u 3 + β 2 ⋅ v 3 + β 1 ⋅ v 3 = f e v e n ( s 1 ( β 2 ) + s 1 ( β 1 ) + s 1 ( 1 )) + ( β 2 + β 1 + 1 ) ⋅ f o dd ( s 1 ( β 2 ) + s 1 ( β 1 ) + s 1 ( 1 )) = u 3 + β 2 ⋅ v 3 + β 1 ⋅ v 3 + v 3 我们把上面这个 Additive FFT 递归算法用 Python 代码实现如下:
def afft(f, k, B):
"""
Perform the Additive Fast Fourier Transform (AFFT) on a given polynomial.
Args:
f (list): Coefficients of the polynomial to be transformed.
k (int): The depth of recursion, where 2^k is the size of the domain.
B (list): The basis of the domain over which the polynomial is evaluated.
Returns:
list: The evaluations of the polynomial over the domain.
"""
if k == 0:
return [f[0]]
half = 2**(k-1)
f_even = f[::2]
f_odd = f[1::2]
V = span(B) # the subspace spanned by B
q = lambda x: x*(x+B[0])/(B[1]*(B[1] + 1)) # s^(i)_1 map
B_half = [q(b) for b in B[1:]] # the basis of the mapped subspace
e_even = afft(f_even, k-1, B_half) # compute the evaluations of f_even
e_odd = afft(f_odd, k-1, B_half) # compute the evaluations of f_odd
e = [0] * (2 * half) # initialize the list of evaluations
for i in range(0, half):
e[2*i] = e_even[i] + V[2*i] * e_odd[i]
e[2*i+1] = e_even[i] + V[2*i+1] * e_odd[i]
return e函数 afft(f, k, B) 总共有三个参数,分别是多项式 f ( X ) f(X) f ( X ) B n o v e l \mathcal{B}^{novel} B n o v e l k k k S ( 0 ) S^{(0)} S ( 0 )
Additive FFT 算法需要一个通过 Subspace Polynomial 构造的子空间的映射链。本文介绍的原理并不局限在递归构造的二进制域,而是一种更广泛的代数结构。
在 [LCH14] 论文中采用的是另外一种递归 Additive FFT 算法,我们将在下一篇文中介绍两者的差异,以及 [DP24] 论文中的 Additive FFT 迭代算法(Algorithm 2)。
References ¶ [DP24] Benjamin E. Diamond and Jim Posen. “Polylogarithmic Proofs for Multilinears over Binary Towers”. 2024. https:// [LCH14] Lin, Sian-Jheng, Wei-Ho Chung, and Yunghsiang S. Han. “Novel polynomial basis and its application to Reed-Solomon erasure codes.” 2014 ieee 55th annual symposium on foundations of computer science. IEEE, 2014. https:// [LN97] Lidl, Rudolf, and Harald Niederreiter. Finite fields. No. 20. Cambridge university press, 1997.