Notes on FRI-Binius (Part I): Binary Towers
二进制域拥有优美的内部结构,而 Binius 是意图充分利用这些内部结构,构造高效的 SNARK 证明系统。本文主要讨论 Binius 底层所依赖的 Binary Fields 以及 基于 Binary Fields 的 Extension Tower 的构造方法。Binary Fields 提供了更小的 Fields,并且兼容传统密码学中的各种工具构造,同时也可以充分利用硬件上的特殊指令的优化。选用 Extension Tower 优点主要有两个,一个是递归的 Extension 构造提供了一致的、增量式的 Basis 选择,从而使得 Small Field 可以以非常自然的方式嵌入到一个 Large Field 中,另一个优点是乘法和求逆运算存在高效的递归算法。
Extension Fields ¶ 我们尝试用简单的语言来描述下 Extension Field 的概念,为后续我们研究 Binary Tower 做铺垫,深入学习请参考有限域教科书中的严格定义和证明。
素数域 F p \mathbb{F}_{p} F p p p p p p p Z / p Z \mathbb{Z}/p\mathbb{Z} Z / p Z { 0 , 1 , … , p − 1 } \{0, 1, \ldots, p-1\} { 0 , 1 , … , p − 1 } F p \mathbb{F}_p F p
我们可以把素数域的任意两个元素组成一个 Tuple,即 ( a , b ) ∈ F p 2 (a, b)\in\mathbb{F}_{p}^2 ( a , b ) ∈ F p 2 p 2 p^2 p 2 a + b ∈ F p a+b\in\mathbb{F}_p a + b ∈ F p
( a 1 , b 1 ) + ( a 2 , b 2 ) = ( a 1 + a 2 , b 1 + b 2 ) (a_1, b_1) + (a_2, b_2) = (a_1 + a_2, b_1 + b_2) ( a 1 , b 1 ) + ( a 2 , b 2 ) = ( a 1 + a 2 , b 1 + b 2 ) 可以验证, F p 2 \mathbb{F}_{p}^2 F p 2 ( 0 , 0 ) (0, 0) ( 0 , 0 )
( a 1 , b 1 ) ⋅ ( a 2 , b 2 ) = ( c , d ) (a_1, b_1)\cdot (a_2, b_2) = (c, d) ( a 1 , b 1 ) ⋅ ( a 2 , b 2 ) = ( c , d ) 一种最简单的做法是采用 Entry-wise Mulplication 来定义乘法,即 ( a 1 , b 1 ) ⋅ ( a 2 , b 2 ) = ( a 1 a 2 , b 1 b 2 ) (a_1, b_1)\cdot (a_2, b_2) = (a_1a_2, b_1b_2) ( a 1 , b 1 ) ⋅ ( a 2 , b 2 ) = ( a 1 a 2 , b 1 b 2 ) ( 1 , 1 ) (1, 1) ( 1 , 1 ) ( 1 , 0 ) (1, 0) ( 1 , 0 ) ( 1 , 1 ) (1, 1) ( 1 , 1 )
在有限域理论中,Tuple 的乘法运算是通过多项式模乘来实现的。也就是我们把 ( a 1 , b 1 ) (a_1, b_1) ( a 1 , b 1 ) ( a 2 , b 2 ) (a_2, b_2) ( a 2 , b 2 )
( a 1 + b 1 ⋅ X ) ⋅ ( a 2 + b 2 ⋅ X ) = a 1 a 2 + ( a 1 b 2 + a 2 b 1 ) X + b 1 b 2 X 2 (a_1 + b_1\cdot X) \cdot (a_2 + b_2\cdot X) = a_1a_2 + (a_1b_2 + a_2b_1)X + b_1b_2X^2 ( a 1 + b 1 ⋅ X ) ⋅ ( a 2 + b 2 ⋅ X ) = a 1 a 2 + ( a 1 b 2 + a 2 b 1 ) X + b 1 b 2 X 2 然后我们再把结果多项式模掉一个 Degree 为 2 的不可约的多项式 f ( X ) f(X) f ( X ) ( c , d ) (c, d) ( c , d )
( a 1 + b 1 ⋅ X ) ⋅ ( a 2 + b 2 ⋅ X ) = c + d ⋅ X m o d f ( X ) (a_1 + b_1\cdot X) \cdot (a_2 + b_2\cdot X) = c + d\cdot X \mod f(X) ( a 1 + b 1 ⋅ X ) ⋅ ( a 2 + b 2 ⋅ X ) = c + d ⋅ X mod f ( X ) 并且定义 ( 1 , 0 ) (1, 0) ( 1 , 0 ) f ( X ) f(X) f ( X ) f ( X ) f(X) f ( X ) f ( X ) = ( u 1 + u 2 X ) ( v 1 + v 2 X ) f(X)=(u_1+u_2X)(v_1+v_2X) f ( X ) = ( u 1 + u 2 X ) ( v 1 + v 2 X ) ( u 1 , u 2 ) (u_1, u_2) ( u 1 , u 2 ) ( v 1 , v 2 ) (v_1, v_2) ( v 1 , v 2 ) ( 0 , 0 ) (0, 0) ( 0 , 0 )
接下来的问题是,是否存在一个不可约的 Degree 为 2 的多项式 f ( X ) f(X) f ( X ) f ( X ) f(X) f ( X ) F p 2 \mathbb{F}_{p^2} F p 2 F p \mathbb{F}_p F p w ∈ F p w\in\mathbb{F}_p w ∈ F p w ∈ Q N R ( p ) w\in QNR(p) w ∈ QNR ( p ) w w w f ( X ) = X 2 − w f(X)=X^2-w f ( X ) = X 2 − w w w w p p p w w w p = 2 p=2 p = 2 w w w f ( X ) = X 2 + X + 1 ∈ F 2 [ X ] f(X)=X^2+X+1\in\mathbb{F}_2[X] f ( X ) = X 2 + X + 1 ∈ F 2 [ X ]
我们现在把 F p 2 \mathbb{F}_{p}^2 F p 2 F p 2 \mathbb{F}_{p^2} F p 2 p 2 p^2 p 2 n n n F p n \mathbb{F}_{p^n} F p n
对于某个 F p \mathbb{F}_p F p f ( X ) = c 0 + c 1 X + X 2 f(X) = c_0 + c_1X + X^2 f ( X ) = c 0 + c 1 X + X 2 F p 2 \mathbb{F}_{p^2} F p 2 f ( X ) = ( X − α ) ( X − α ′ ) f(X) = (X-\alpha)(X-\alpha') f ( X ) = ( X − α ) ( X − α ′ ) α \alpha α α ′ \alpha' α ′ F p 2 \mathbb{F}_{p^2} F p 2 F p \mathbb{F}_p F p F p ( α ) \mathbb{F}_p(\alpha) F p ( α ) a 1 + a 2 ⋅ α a_1 + a_2\cdot\alpha a 1 + a 2 ⋅ α F p 2 \mathbb{F}_{p^2} F p 2 ( 1 , α ) (1, \alpha) ( 1 , α ) F p 2 \mathbb{F}_{p^2} F p 2 a ∈ F p 2 a\in \mathbb{F}_{p^2} a ∈ F p 2
a = a 0 ⋅ 1 + a 1 ⋅ α , a 0 , a 1 ∈ F p a = a_0 \cdot 1 + a_1 \cdot \alpha, \quad a_0, a_1\in\mathbb{F}_p a = a 0 ⋅ 1 + a 1 ⋅ α , a 0 , a 1 ∈ F p 这样一来,我们就可以用符号 a 0 + a 1 ⋅ α a_0 + a_1\cdot \alpha a 0 + a 1 ⋅ α F p 2 \mathbb{F}_{p^2} F p 2 a 0 + a 1 ⋅ X a_0 + a_1\cdot X a 0 + a 1 ⋅ X α \alpha α
把这个概念推广到 F p n \mathbb{F}_{p^n} F p n a ∈ F p n a\in\mathbb{F}_{p^n} a ∈ F p n
a = a 0 + a 1 ⋅ α + a 2 ⋅ α 2 + ⋯ + a n − 1 ⋅ α n − 1 a = a_0 + a_1\cdot\alpha + a_2\cdot\alpha^2 + \cdots + a_{n-1}\cdot\alpha^{n-1} a = a 0 + a 1 ⋅ α + a 2 ⋅ α 2 + ⋯ + a n − 1 ⋅ α n − 1 这里 α \alpha α n n n f ( X ) f(X) f ( X ) ( 1 , α , α 2 , ⋯ , α n − 1 ) (1, \alpha, \alpha^2, \cdots, \alpha^{n-1}) ( 1 , α , α 2 , ⋯ , α n − 1 ) F p n \mathbb{F}_{p^n} F p n F p n \mathbb{F}_{p^n} F p n n n n
TODO: Fp* 乘法循环群
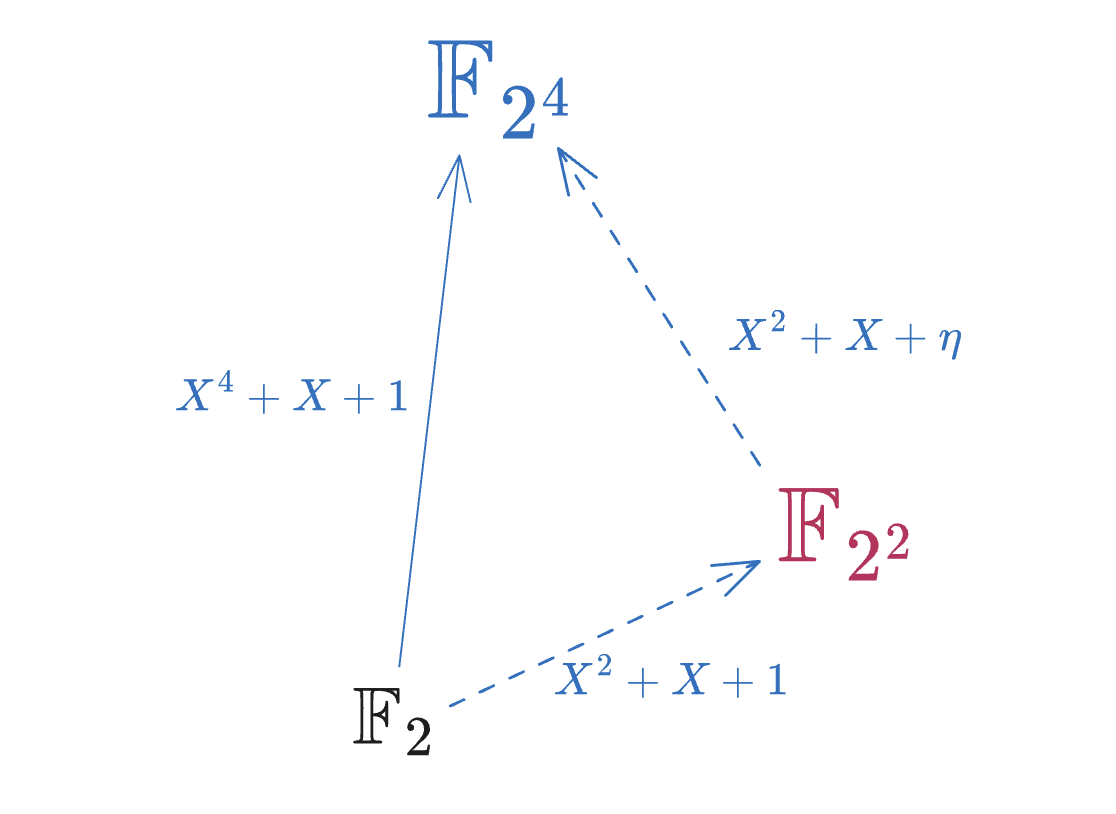
Binary Field ¶ 对于 F 2 n \mathbb{F}_{2^n} F 2 n n n n F 2 n \mathbb{F}_{2^n} F 2 n n n n 2 n 2^n 2 n F 2 8 \mathbb{F}_{2^8} F 2 8 F 2 4 \mathbb{F}_{2^4} F 2 4 F 2 8 \mathbb{F}_{2^8} F 2 8 F 2 2 \mathbb{F}_{2^2} F 2 2 F 2 8 \mathbb{F}_{2^8} F 2 8
我们先热身下,利用二次扩张的方法构造 F 2 2 \mathbb{F}_{2^2} F 2 2 f ( X ) = X 2 + X + 1 f(X)=X^2+X+1 f ( X ) = X 2 + X + 1 F 2 [ X ] \mathbb{F}_2[X] F 2 [ X ] η \eta η f ( X ) f(X) f ( X ) F 2 2 \mathbb{F}_{2^2} F 2 2 a 0 + b 0 ⋅ η a_0 + b_0\cdot\eta a 0 + b 0 ⋅ η F 2 2 \mathbb{F}_{2^2} F 2 2
F 2 2 = { 0 , 1 , η , η + 1 } \mathbb{F}_{2^2} = \{0, 1, \eta, \eta+1\} F 2 2 = { 0 , 1 , η , η + 1 } 并且 η \eta η F 2 2 ∗ = ⟨ η ⟩ \mathbb{F}_{2^2}^*=\langle \eta \rangle F 2 2 ∗ = ⟨ η ⟩
η 0 = 1 η 1 = η η 2 = η + 1 \begin{split}
\eta^0 &= 1 \\
\eta^1 &= \eta \\
\eta^2 &= \eta+1 \\
\end{split} η 0 η 1 η 2 = 1 = η = η + 1 我们演示下 F 2 4 \mathbb{F}_{2^4} F 2 4 F 2 \mathbb{F}_2 F 2
f 1 ( X ) = X 4 + X + 1 f 2 ( X ) = X 4 + X 3 + 1 f 3 ( X ) = X 4 + X 3 + X 2 + X + 1 \begin{split}
f_1(X) &= X^4 + X + 1 \\
f_2(X) &= X^4 + X^3 + 1 \\
f_3(X) &= X^4 + X^3 + X^2 + X + 1 \\
\end{split} f 1 ( X ) f 2 ( X ) f 3 ( X ) = X 4 + X + 1 = X 4 + X 3 + 1 = X 4 + X 3 + X 2 + X + 1 因为只需要选择一个不可约多项式即可,那我们就选择 f 1 ( X ) f_1(X) f 1 ( X ) F 2 4 \mathbb{F}_{2^4} F 2 4
F 2 4 = F 2 [ X ] / ⟨ f 1 ( X ) ⟩ \mathbb{F}_{2^4} = \mathbb{F}_2[X]/\langle f_1(X)\rangle F 2 4 = F 2 [ X ] / ⟨ f 1 ( X )⟩ 我们把 f 1 ( X ) f_1(X) f 1 ( X ) F 2 4 \mathbb{F}_{2^4} F 2 4 θ \theta θ a ∈ F 2 4 a\in\mathbb{F}_{2^4} a ∈ F 2 4
a = a 0 + a 1 ⋅ θ + a 2 ⋅ θ 2 + ⋯ + a n − 1 ⋅ θ n − 1 a = a_0 + a_1\cdot\theta + a_2\cdot\theta^2 + \cdots + a_{n-1}\cdot\theta^{n-1} a = a 0 + a 1 ⋅ θ + a 2 ⋅ θ 2 + ⋯ + a n − 1 ⋅ θ n − 1 这里补充一下,f 1 ( X ) f_1(X) f 1 ( X ) θ \theta θ F 2 4 \mathbb{F}_{2^4} F 2 4 f 3 ( X ) f_3(X) f 3 ( X )
下面我们可以列出 F 2 4 \mathbb{F}_{2^4} F 2 4
0000 0001 0010 0011 0100 0101 0110 0111 0 1 θ θ + 1 θ 2 θ 2 + 1 θ 2 + θ θ 2 + θ + 1 1000 1001 1010 1011 1100 1101 1110 1111 θ 3 θ 3 + 1 θ 3 + θ θ 3 + θ + 1 θ 3 + θ 2 θ 3 + θ 2 + 1 θ 3 + θ 2 + θ θ 3 + θ 2 + θ + 1 \begin{array}{cccccccc}
0000 & 0001 & 0010 & 0011 & 0100 & 0101 & 0110 & 0111 \\
0 & 1 & \theta & \theta+1 & \theta^2 & \theta^2+1 & \theta^2+\theta & \theta^2+\theta+1 \\
\hline
1000 & 1001 & 1010 & 1011 & 1100 & 1101 & 1110 & 1111 \\
\theta^3 & \theta^3+1 & \theta^3+\theta & \theta^3+\theta+1 & \theta^3+\theta^2 & \theta^3+\theta^2+1 & \theta^3+\theta^2+\theta & \theta^3+\theta^2+\theta+1 \\
\end{array} 0000 0 1000 θ 3 0001 1 1001 θ 3 + 1 0010 θ 1010 θ 3 + θ 0011 θ + 1 1011 θ 3 + θ + 1 0100 θ 2 1100 θ 3 + θ 2 0101 θ 2 + 1 1101 θ 3 + θ 2 + 1 0110 θ 2 + θ 1110 θ 3 + θ 2 + θ 0111 θ 2 + θ + 1 1111 θ 3 + θ 2 + θ + 1 对于 F 2 4 \mathbb{F}_{2^4} F 2 4
( 0101 ) + ( 1111 ) = ( 1010 ) (0101) + (1111) = (1010) ( 0101 ) + ( 1111 ) = ( 1010 ) 这个运算实际上就是 XOR 按位异或运算。而对于乘法,比如 a ⋅ θ a\cdot\theta a ⋅ θ
( 0101 ) < < 1 = ( 1010 ) ( θ 2 + 1 ) ⋅ θ = θ 3 + θ \begin{split}
(0101) << 1 &= (1010)\\
(\theta^2 + 1)\cdot\theta &= \theta^3 + \theta \\
\end{split} ( 0101 ) << 1 ( θ 2 + 1 ) ⋅ θ = ( 1010 ) = θ 3 + θ 如果继续乘以 θ \theta θ
( θ 3 + θ ) ⋅ θ = θ 4 + θ 2 = θ 2 + θ + 1 ( 1010 ) < < 1 = ( 0100 ) + ( 0011 ) = ( 0111 ) \begin{split}
(\theta^3 + \theta)\cdot\theta &= {\color{blue}\theta^4} + \theta^2 = \theta^2 + \theta + 1 \\
(1010) << 1 &= (0100) + (0011) = (0111)\\
\end{split} ( θ 3 + θ ) ⋅ θ ( 1010 ) << 1 = θ 4 + θ 2 = θ 2 + θ + 1 = ( 0100 ) + ( 0011 ) = ( 0111 ) 对于溢出位,则需要补加上 0011,这是由不可约多项式 f 1 ( X ) f_1(X) f 1 ( X ) θ 4 = θ + 1 \theta^4=\theta+1 θ 4 = θ + 1 F 2 4 \mathbb{F}_{2^4} F 2 4
Field Embedding ¶ 如果我们要基于二进制域的构造 SNARK 证明系统,我们会将较小的数字用小位数来表示,但是不管怎么样,在协议的挑战轮,Verifier 都要给出一个在较大的扩张域中的随机数,以期望达到足够的密码学安全强度。这就需要我们在小域中用多项式编码 witness 信息,但在一个较大的域中对这些多项式进行取值运算。那么,我们需要找到一种办法把小域 K K K L L L
所谓的嵌入(Embedding),指的是把一个域 K K K L L L ϕ : K → L \phi: K\to L ϕ : K → L
ϕ ( a + b ) = ϕ ( a ) + ϕ ( b ) ϕ ( a ⋅ b ) = ϕ ( a ) ⋅ ϕ ( b ) \begin{split}
\phi(a+b) &= \phi(a) + \phi(b) \\
\phi(a\cdot b) &= \phi(a)\cdot\phi(b)
\end{split} ϕ ( a + b ) ϕ ( a ⋅ b ) = ϕ ( a ) + ϕ ( b ) = ϕ ( a ) ⋅ ϕ ( b ) 即如果 a ∈ K a\in K a ∈ K a a a L L L α \alpha α L L L β \beta β K K K α \alpha α F 2 2 ⊂ F 2 4 \mathbb{F}_{2^2}\subset\mathbb{F}_{2^4} F 2 2 ⊂ F 2 4
因为 η \eta η F 2 2 \mathbb{F}_{2^2} F 2 2 η \eta η F 2 4 \mathbb{F}_{2^4} F 2 4
我们先看看 F 2 4 \mathbb{F}_{2^4} F 2 4 θ \theta θ η ↦ θ \eta\mapsto\theta η ↦ θ
η 2 = η + 1 but θ 2 ≠ θ + 1 \eta^2 = \eta+1 \quad \text{but} \quad \theta^2 \neq \theta+1 η 2 = η + 1 but θ 2 = θ + 1 很显然,η 2 ≠ θ 2 \eta^2 \neq \theta^2 η 2 = θ 2 η ↦ θ \eta\mapsto\theta η ↦ θ η \eta η X 2 + X + 1 X^2+X+1 X 2 + X + 1 θ \theta θ X 4 + X + 1 X^4+X+1 X 4 + X + 1 η \eta η θ \theta θ F 2 4 \mathbb{F}_{2^4} F 2 4 X 2 + X + 1 X^2+X+1 X 2 + X + 1 θ 2 + θ \theta^2+\theta θ 2 + θ θ 2 + θ + 1 \theta^2+\theta+1 θ 2 + θ + 1
( θ 2 + θ ) 2 + ( θ 2 + θ ) + 1 = θ 4 + θ 2 + θ 2 + θ + 1 = 0 (\theta^2+\theta)^2 + (\theta^2+\theta) + 1 = \theta^4 + \theta^2 + \theta^2 + \theta + 1 = 0 ( θ 2 + θ ) 2 + ( θ 2 + θ ) + 1 = θ 4 + θ 2 + θ 2 + θ + 1 = 0 那么,我们就定义嵌入映射:
ϕ : F 2 2 → F 2 4 , η ↦ θ 2 + θ \begin{split}
\phi &: \mathbb{F}_{2^2} \to \mathbb{F}_{2^4},\quad \eta \mapsto \theta^2+\theta
\end{split} ϕ : F 2 2 → F 2 4 , η ↦ θ 2 + θ 这就意味着二进制 ( 10 ) (10) ( 10 ) L = F 2 4 L=\mathbb{F}_{2^4} L = F 2 4 ( 0110 ) (0110) ( 0110 ) ( 11 ) (11) ( 11 ) η + 1 \eta+1 η + 1 L L L ( θ 2 + θ + 1 ) (\theta^2+\theta+1) ( θ 2 + θ + 1 ) ( 0111 ) (0111) ( 0111 ) ϕ ′ : η ↦ θ 2 + θ + 1 \phi': \eta \mapsto \theta^2+\theta+1 ϕ ′ : η ↦ θ 2 + θ + 1 θ 2 + θ \theta^2+\theta θ 2 + θ θ 2 + θ + 1 \theta^2+\theta+1 θ 2 + θ + 1
而对于任意的 [ L : K ] = n [L:K]=n [ L : K ] = n K K K L L L f ( X ) f(X) f ( X ) L L L
而 Binius 论文提到的采用递归式 Extension Tower 的构造方法,通过选取合适的不可约多项式和 Basis,我们就可以得到非常直接(称为 Zero-cost)的嵌入和反嵌入映射。
Extension Tower ¶ 我们可以通过两次的二次扩张来构造 F 2 4 \mathbb{F}_{2^4} F 2 4 f ( X ) = X 2 + X + 1 f(X)=X^2+X+1 f ( X ) = X 2 + X + 1 F 2 2 \mathbb{F}_{2^2} F 2 2 F 2 2 \mathbb{F}_{2^2} F 2 2 F 2 4 \mathbb{F}_{2^4} F 2 4
F 2 2 = F 2 [ X ] / ⟨ X 2 + X + 1 ⟩ ≅ F 2 ( η ) \mathbb{F}_{2^2} = \mathbb{F}_2[X]/\langle X^2+X+1 \rangle \cong\mathbb{F}_2(\eta) F 2 2 = F 2 [ X ] / ⟨ X 2 + X + 1 ⟩ ≅ F 2 ( η ) 接下我们要找到 F 2 2 [ X ] \mathbb{F}_{2^2}[X] F 2 2 [ X ] X 2 + X + 1 X^2+X+1 X 2 + X + 1 F 2 2 \mathbb{F}_{2^2} F 2 2 X 2 + 1 X^2+1 X 2 + 1 ( X + 1 ) ( X + 1 ) (X+1)(X+1) ( X + 1 ) ( X + 1 ) F 2 [ X ] \mathbb{F}_2[X] F 2 [ X ] F 2 2 [ X ] \mathbb{F}_{2^2}[X] F 2 2 [ X ] η \eta η
比如 X 2 + X + η X^2+X+\eta X 2 + X + η F 2 2 \mathbb{F}_{2^2} F 2 2 F 2 4 \mathbb{F}_{2^4} F 2 4
F 2 4 = F 2 2 [ X ] / ⟨ X 2 + X + η ⟩ \mathbb{F}_{2^4} = \mathbb{F}_{2^2}[X]/\langle X^2+X+\eta \rangle F 2 4 = F 2 2 [ X ] / ⟨ X 2 + X + η ⟩ 我们把 X 2 + X + η X^2+X+\eta X 2 + X + η F 2 4 \mathbb{F}_{2^4} F 2 4 ζ \zeta ζ F 2 4 \mathbb{F}_{2^4} F 2 4
F 2 4 ≅ F 2 2 ( ζ ) ≅ F 2 ( η ) ( ζ ) ≅ F 2 ( η , ζ ) \mathbb{F}_{2^4} \cong \mathbb{F}_{2^2}(\zeta) \cong \mathbb{F}_2(\eta)(\zeta) \cong \mathbb{F}_2(\eta, \zeta) F 2 4 ≅ F 2 2 ( ζ ) ≅ F 2 ( η ) ( ζ ) ≅ F 2 ( η , ζ ) 那么 F 2 4 \mathbb{F}_{2^4} F 2 4 η , ζ \eta, \zeta η , ζ
0000 0001 0010 0011 0100 0101 0110 0111 0 1 η η + 1 ζ ζ + 1 ζ + η ζ + η + 1 1000 1001 1010 1011 1100 1101 1110 1111 ζ η ζ η + 1 ζ η + η ζ η + η + 1 ζ η + ζ ζ η + ζ + 1 ζ η + ζ + η ζ η + ζ + η + 1 \begin{array}{cccccccc}
\hline
0000 & 0001 & 0010 & 0011 & 0100 & 0101 & 0110 & 0111 \\
0 & 1 & \eta & \eta+1 & \zeta & \zeta+1 & \zeta+\eta & \zeta+\eta+1 \\
\hline
1000 & 1001 & 1010 & 1011 & 1100 & 1101 & 1110 & 1111 \\
\zeta\eta & \zeta\eta + 1 & \zeta\eta + \eta & \zeta\eta + \eta + 1 & \zeta\eta + \zeta & \zeta\eta + \zeta +1 & \zeta\eta+\zeta+\eta & \zeta\eta+\zeta+\eta+1 \\
\hline
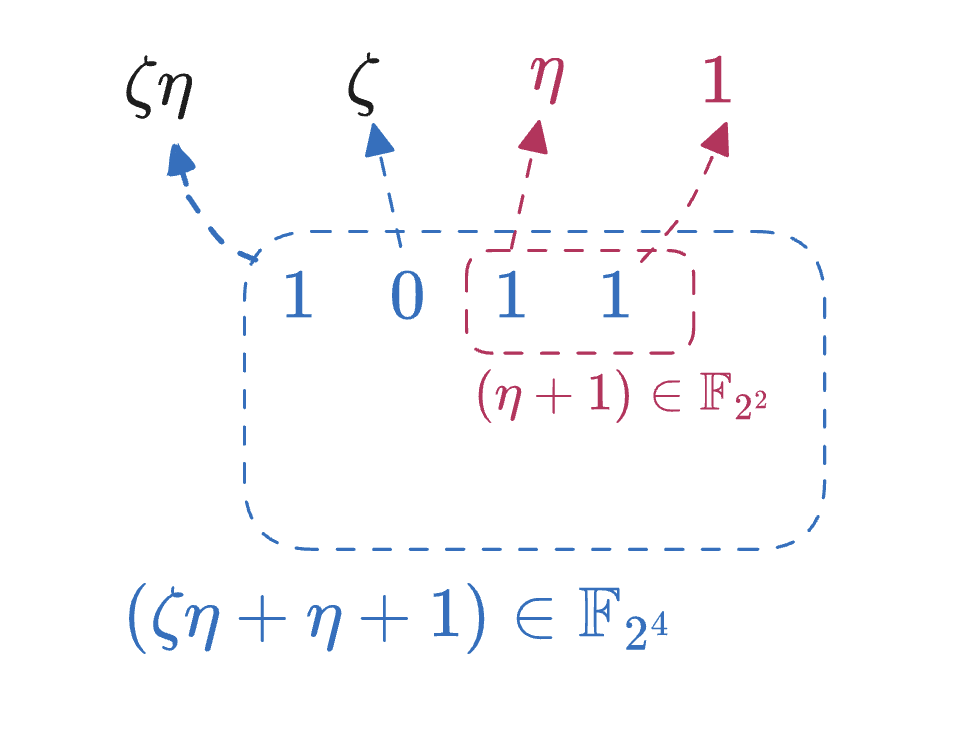
\end{array} 0000 0 1000 ζ η 0001 1 1001 ζ η + 1 0010 η 1010 ζ η + η 0011 η + 1 1011 ζ η + η + 1 0100 ζ 1100 ζ η + ζ 0101 ζ + 1 1101 ζ η + ζ + 1 0110 ζ + η 1110 ζ η + ζ + η 0111 ζ + η + 1 1111 ζ η + ζ + η + 1 这时,4bit 二进制中的每一个 bit 都对应于 F 2 4 \mathbb{F}_{2^4} F 2 4 ( 1000 ) (1000) ( 1000 ) ζ η \zeta\eta ζ η ( 0100 ) (0100) ( 0100 ) ζ \zeta ζ ( 0010 ) (0010) ( 0010 ) η \eta η ( 0001 ) (0001) ( 0001 ) F 2 4 \mathbb{F}_{2^4} F 2 4
B = ( 1 , η , ζ , η ζ ) \mathcal{B} = (1,\ \eta,\ \zeta,\ \eta\zeta) B = ( 1 , η , ζ , η ζ ) 这时候,F 2 2 \mathbb{F}_{2^2} F 2 2 F 2 4 \mathbb{F}_{2^4} F 2 4
( 1010 ) = ( 10 ) ∣ ∣ ( 10 ) = ζ η + η \begin{split}
(1010) &= (10) || (10) = \zeta\eta + \eta \\
\end{split} ( 1010 ) = ( 10 ) ∣∣ ( 10 ) = ζ η + η 因此,我们可以直接在 F 2 2 \mathbb{F}_{2^2} F 2 2 F 2 4 \mathbb{F}_{2^4} F 2 4 F 2 4 \mathbb{F}_{2^4} F 2 4 F 2 2 \mathbb{F}_{2^2} F 2 2
如上图所示,( 1011 ) (1011) ( 1011 ) ζ η + η + 1 \zeta\eta+\eta+1 ζ η + η + 1 ( 11 ) (11) ( 11 ) F 2 2 \mathbb{F}_{2^2} F 2 2 ( η + 1 ) (\eta+1) ( η + 1 )
不过 F 2 4 \mathbb{F}_{2^4} F 2 4
Wiedemann Tower ¶ Wiedemann Tower 是一个基于 F 2 \mathbb{F}_2 F 2 T 0 \mathcal{T}_0 T 0
T 0 = F 2 ≅ { 0 , 1 } \mathcal{T}_0 = \mathbb{F}_2 \cong \{0,1\} T 0 = F 2 ≅ { 0 , 1 } 然后我们引入一个未知数 X 0 X_0 X 0 F 2 [ X 0 ] \mathbb{F}_2[X_0] F 2 [ X 0 ] X 2 + X + 1 X^2 + X + 1 X 2 + X + 1 T 0 \mathcal{T}_0 T 0 T 1 \mathcal{T}_1 T 1
T 1 = F 2 [ X 0 ] / ⟨ X 0 2 + X 0 + 1 ⟩ = { 0 , 1 , X 0 , X 0 + 1 } ≅ F 2 2 ≅ F 2 ( α 0 ) \mathcal{T}_1 = \mathbb{F}_2[X_0]/\langle X_0^2+X_0+1 \rangle = \{0, 1, X_0, X_0+1\} \cong \mathbb{F}_{2^2} \cong \mathbb{F}_2(\alpha_0) T 1 = F 2 [ X 0 ] / ⟨ X 0 2 + X 0 + 1 ⟩ = { 0 , 1 , X 0 , X 0 + 1 } ≅ F 2 2 ≅ F 2 ( α 0 ) 接下来,我们找到一个 T 1 [ X 1 ] \mathcal{T}_1[X_1] T 1 [ X 1 ] X 1 2 + α 0 ⋅ X 1 + 1 X_1^2+\alpha_0\cdot X_1+1 X 1 2 + α 0 ⋅ X 1 + 1 T 2 \mathcal{T}_2 T 2
T 2 = T 1 [ X 1 ] / ⟨ X 1 2 + α 0 ⋅ X 1 + 1 ⟩ ≅ F 2 4 ≅ F 2 ( α 0 , α 1 ) \mathcal{T}_2 = \mathcal{T}_1[X_1]/\langle X_1^2+ \alpha_0\cdot X_1+1\rangle \cong \mathbb{F}_{2^4} \cong \mathbb{F}_2(\alpha_0, \alpha_1) T 2 = T 1 [ X 1 ] / ⟨ X 1 2 + α 0 ⋅ X 1 + 1 ⟩ ≅ F 2 4 ≅ F 2 ( α 0 , α 1 ) 依次类推,我们可以构造出 T 3 , T 4 , ⋯ , T n \mathcal{T}_3, \mathcal{T}_4, \cdots, \mathcal{T}_n T 3 , T 4 , ⋯ , T n
T i + 1 = T i [ X i ] / ⟨ X i 2 + α i − 1 ⋅ X i + 1 ⟩ ≅ F 2 2 i ≅ F 2 ( α 0 , α 1 , … , α i ) , i ≥ 1 \mathcal{T}_{i+1} = \mathcal{T}_i[X_i]/\langle X_i^2+\alpha_{i-1}\cdot X_i+1\rangle \cong \mathbb{F}_{2^{2^i}} \cong \mathbb{F}_2(\alpha_0, \alpha_1, \ldots, \alpha_i),\quad i\geq 1 T i + 1 = T i [ X i ] / ⟨ X i 2 + α i − 1 ⋅ X i + 1 ⟩ ≅ F 2 2 i ≅ F 2 ( α 0 , α 1 , … , α i ) , i ≥ 1 这里,α 0 , α 1 , … , α n − 1 \alpha_0, \alpha_1, \ldots, \alpha_{n-1} α 0 , α 1 , … , α n − 1
T n = F 2 ( α 0 , α 1 , … , α n − 1 ) \mathcal{T}_{n} = \mathbb{F}_2(\alpha_0, \alpha_1, \ldots, \alpha_{n-1}) T n = F 2 ( α 0 , α 1 , … , α n − 1 ) 而 ∣ T n ∣ = 2 2 n |\mathcal{T}_{n}| = 2^{2^{n}} ∣ T n ∣ = 2 2 n
α i + 1 + α i + 1 − 1 = α i \alpha_{i+1} + \alpha^{-1}_{i+1} = \alpha_i α i + 1 + α i + 1 − 1 = α i 不难检验,α 0 + α 0 − 1 = 1 \alpha_0+\alpha^{-1}_0=1 α 0 + α 0 − 1 = 1 T 0 [ X 0 , X 1 , … , X n ] \mathcal{T}_0[X_0, X_1, \ldots, X_n] T 0 [ X 0 , X 1 , … , X n ] X i 2 + X i − 1 X i + 1 X_i^2+X_{i-1}X_i+1 X i 2 + X i − 1 X i + 1 α i \alpha_i α i α i − 1 \alpha^{-1}_i α i − 1
( α i − 1 ) 2 + α i − 1 α i − 1 + 1 = α i − 1 + α i − 1 + α i = α i − 1 + α i − 1 = 0 (\alpha^{-1}_i)^2 + \alpha_{i-1}\alpha^{-1}_i + 1 = \alpha^{-1}_i + \alpha_{i-1} + \alpha_i = \alpha_{i-1} + \alpha_{i-1} = 0 ( α i − 1 ) 2 + α i − 1 α i − 1 + 1 = α i − 1 + α i − 1 + α i = α i − 1 + α i − 1 = 0 并且,α i \alpha_i α i α i + 1 \alpha_{i+1} α i + 1
α i + 1 + α i + 1 − 1 = α i \alpha_{i+1} + \alpha^{-1}_{i+1} = \alpha_i α i + 1 + α i + 1 − 1 = α i 这是因为等式两边都乘以 α i + 1 \alpha_{i+1} α i + 1 α i + 1 2 + α i α i + 1 + 1 = 0 \alpha_{i+1}^2 + \alpha_i\alpha_{i+1} + 1 = 0 α i + 1 2 + α i α i + 1 + 1 = 0
Multilinear Basis ¶ 对于 T i + 1 \mathcal{T}_{i+1} T i + 1 F 2 \mathbb{F}_2 F 2 F 2 \mathbb{F}_2 F 2 n + 1 n+1 n + 1
B i + 1 = ( 1 , α 0 ) ⊗ ( 1 , α 1 ) ⊗ ⋯ ⊗ ( 1 , α i ) = ( 1 , α 0 , α 1 , α 0 α 1 , α 2 , … , α 0 α 1 ⋯ α i ) \begin{split}
\mathcal{B}_{i+1} &= (1, \alpha_0)\otimes (1, \alpha_1) \otimes \cdots \otimes (1,\alpha_i) \\
& = (1, \alpha_0, \alpha_1, \alpha_0\alpha_1, \alpha_2,\ \ldots,\ \alpha_0\alpha_1\cdots \alpha_i)
\end{split} B i + 1 = ( 1 , α 0 ) ⊗ ( 1 , α 1 ) ⊗ ⋯ ⊗ ( 1 , α i ) = ( 1 , α 0 , α 1 , α 0 α 1 , α 2 , … , α 0 α 1 ⋯ α i ) 这与我们前面讨论过的,使用 ( 1 , η , ζ , ζ η ) (1, \eta, \zeta, \zeta\eta) ( 1 , η , ζ , ζ η ) F 2 ( η , ζ ) \mathbb{F}_{2}(\eta, \zeta) F 2 ( η , ζ ) ( 1 , α 0 ) (1, \alpha_0) ( 1 , α 0 ) T 1 \mathcal{T}_1 T 1 T 1 \mathcal{T}_1 T 1
a 0 + b 0 ⋅ α 0 , a 0 , b 0 ∈ T 0 a_0 + b_0\cdot \alpha_0, \quad a_0, b_0\in\mathcal{T}_0 a 0 + b 0 ⋅ α 0 , a 0 , b 0 ∈ T 0 当 T 1 \mathcal{T}_1 T 1 α 1 \alpha_1 α 1 T 2 \mathcal{T}_2 T 2 T 2 \mathcal{T}_2 T 2
a 1 + b 1 ⋅ α 1 , a 1 , b 1 ∈ T 1 a_1 + b_1\cdot \alpha_1, \quad a_1, b_1\in\mathcal{T}_1 a 1 + b 1 ⋅ α 1 , a 1 , b 1 ∈ T 1 代入 a 1 = a 0 + b 0 ⋅ α 0 a_1=a_0+b_0\cdot \alpha_0 a 1 = a 0 + b 0 ⋅ α 0 b 1 = a 0 ′ + b 0 ′ ⋅ α 1 b_1=a_0'+b_0'\cdot \alpha_1 b 1 = a 0 ′ + b 0 ′ ⋅ α 1
a 1 + b 1 ⋅ α 1 = ( a 0 + b 0 ⋅ α 0 ) + ( a 0 ′ + b 0 ′ ⋅ α 0 ) ⋅ α 1 = a 0 + b 0 α 0 + a 0 ′ ⋅ α 1 + b 0 ′ ⋅ α 0 α 1 \begin{split}
a_1 + b_1\cdot \alpha_1 &= (a_0+b_0\cdot \alpha_0) + (a'_0+b'_0\cdot \alpha_0)\cdot \alpha_1 \\
&= a_0 + b_0\alpha_0 + a'_0\cdot\alpha_1+ b_0'\cdot \alpha_0\alpha_1
\end{split} a 1 + b 1 ⋅ α 1 = ( a 0 + b 0 ⋅ α 0 ) + ( a 0 ′ + b 0 ′ ⋅ α 0 ) ⋅ α 1 = a 0 + b 0 α 0 + a 0 ′ ⋅ α 1 + b 0 ′ ⋅ α 0 α 1 于是,( 1 , α 0 , α 1 , α 0 α 1 ) (1, \alpha_0, \alpha_1, \alpha_0\alpha_1) ( 1 , α 0 , α 1 , α 0 α 1 ) T 2 \mathcal{T}_2 T 2 ( 1 , α 0 , α 1 , α 0 α 1 , α 2 , α 0 α 2 , α 1 α 2 , α 0 α 1 α 2 ) (1, \alpha_0, \alpha_1, \alpha_0\alpha_1, \alpha_2, \alpha_0\alpha_2, \alpha_1\alpha_2, \alpha_0\alpha_1\alpha_2) ( 1 , α 0 , α 1 , α 0 α 1 , α 2 , α 0 α 2 , α 1 α 2 , α 0 α 1 α 2 ) T 3 \mathcal{T}_3 T 3 B n \mathcal{B}_{n} B n T n \mathcal{T}_{n} T n
寻找 Primitive element ¶ 前面我们讨论过 α i \alpha_i α i α i − 1 \alpha^{-1}_{i} α i − 1
α i 2 2 n = α i − 1 \alpha_{i}^{2^{2^n}} = \alpha^{-1}_{i} α i 2 2 n = α i − 1 那么 α i \alpha_i α i
α i F i = 1 \alpha_i^{F_i} = 1 α i F i = 1 这里 F n F_n F n F n = 2 2 n + 1 F_n=2^{2^n}+1 F n = 2 2 n + 1 g c d ( F i , F j ) = 1 , i ≠ j \mathsf{gcd}(F_i, F_j) = 1, i\neq j gcd ( F i , F j ) = 1 , i = j
o r d ( α 0 α 1 ⋯ α i ) = o r d ( α 0 ) o r d ( α 1 ) ⋯ o r d ( α i ) \mathsf{ord}(\alpha_0\alpha_1\cdots \alpha_i) = \mathsf{ord}(\alpha_0)\mathsf{ord}(\alpha_1)\cdots\mathsf{ord}(\alpha_i) ord ( α 0 α 1 ⋯ α i ) = ord ( α 0 ) ord ( α 1 ) ⋯ ord ( α i ) 因此,如果费马数 F i F_i F i o r d ( α i ) = F i \mathsf{ord}(\alpha_i)=F_i ord ( α i ) = F i i ≤ 4 i\leq 4 i ≤ 4 F i F_i F i
o r d ( α 0 ⋅ α 1 ⋅ ⋯ ⋅ α i ) = o r d ( α 0 ) ⋅ o r d ( α 1 ) ⋅ ⋯ ⋅ o r d ( α n ) = F 0 ⋅ F 1 ⋅ ⋯ ⋅ F i = 2 2 i + 1 − 1 = ∣ T n + 1 ∣ − 1 \begin{split}
\mathsf{ord}(\alpha_0\cdot \alpha_1\cdot \cdots \cdot \alpha_i) &= \mathsf{ord}(\alpha_0)\cdot \mathsf{ord}(\alpha_1)\cdot \cdots \cdot \mathsf{ord}(\alpha_n) \\
& = F_0\cdot F_1\cdot \cdots \cdot F_i = 2^{2^{i+1}} - 1 \\
& = |\mathcal{T}_{n+1}| -1
\end{split} ord ( α 0 ⋅ α 1 ⋅ ⋯ ⋅ α i ) = ord ( α 0 ) ⋅ ord ( α 1 ) ⋅ ⋯ ⋅ ord ( α n ) = F 0 ⋅ F 1 ⋅ ⋯ ⋅ F i = 2 2 i + 1 − 1 = ∣ T n + 1 ∣ − 1 如果 α 0 ⋯ α i , i ≤ 4 \alpha_0\cdots \alpha_i, i\leq 4 α 0 ⋯ α i , i ≤ 4 T n + 1 \mathcal{T}_{n+1} T n + 1
另外,通过计算机程序检查验证,对于 5 ≤ i ≤ 8 5\leq i \leq 8 5 ≤ i ≤ 8 α i \alpha_i α i F i F_i F i α 0 ⋯ α 8 \alpha_0\cdots \alpha_8 α 0 ⋯ α 8 F 2 512 \mathbb{F}_{2^{512}} F 2 512 α i \alpha_i α i
乘法优化 ¶ 采用 Extension Tower 的另一个显著的优点是乘法运算的优化。
第一种优化是 “Small-by-large Multiplication”,即 a ∈ T ι a\in\mathcal{T}_\iota a ∈ T ι b ∈ T ι + κ b\in\mathcal{T}_{\iota+\kappa} b ∈ T ι + κ b b b 2 κ 2^\kappa 2 κ T ι \mathcal{T}_\iota T ι 2 κ 2^\kappa 2 κ T ι \mathcal{T}_\iota T ι
a ⋅ ( b 0 , b 1 , ⋯ , b 2 κ − 1 ) = ( a ⋅ b 0 , a ⋅ b 1 , ⋯ , a ⋅ b κ − 1 ) a \cdot (b_0, b_1, \cdots, b_{2^\kappa-1}) = (a\cdot b_0, a\cdot b_1, \cdots, a\cdot b_{\kappa-1}) a ⋅ ( b 0 , b 1 , ⋯ , b 2 κ − 1 ) = ( a ⋅ b 0 , a ⋅ b 1 , ⋯ , a ⋅ b κ − 1 ) 即使对于同一个域上的两个元素的乘法,也同样有优化手段。假设 a , b ∈ T i + 1 a, b\in\mathcal{T}_{i+1} a , b ∈ T i + 1 a 0 + a 1 ⋅ α i a_0 + a_1\cdot\alpha_i a 0 + a 1 ⋅ α i b 0 + b 1 ⋅ α i b_0 + b_1\cdot \alpha_i b 0 + b 1 ⋅ α i
a ⋅ b = ( a 0 + a 1 ⋅ α i ) ⋅ ( b 0 + b 1 ⋅ α i ) = a 0 b 0 + ( a 0 b 1 + a 1 b 0 ) ⋅ α i + a 1 b 1 ⋅ α i 2 = a 0 b 0 + ( a 0 b 1 + a 1 b 0 ) ⋅ α i + a 1 b 1 ⋅ ( α i − 1 α i + 1 ) = a 0 b 0 + a 1 b 1 + ( a 0 b 1 + a 1 b 0 + a 1 b 1 ⋅ α i − 1 ) ⋅ α i = a 0 b 0 + a 1 b 1 + ( ( a 0 + a 1 ) ( b 0 + b 1 ) − a 0 b 0 − a 1 b 1 ) + a 1 b 1 ⋅ α i − 1 ) ⋅ α i \begin{split}
a\cdot b & = (a_0 + a_1\cdot\alpha_i)\cdot (b_0 + b_1\cdot\alpha_i) \\
&= a_0b_0 + (a_0b_1+a_1b_0)\cdot\alpha_i + a_1b_1\cdot\alpha_i^2 \\
& = a_0b_0 + (a_0b_1+a_1b_0)\cdot\alpha_i + a_1b_1\cdot(\alpha_{i-1}\alpha_i+1) \\
& = a_0b_0 + a_1b_1 + (a_0b_1 + a_1b_0 + a_1b_1\cdot\alpha_{i-1})\cdot\alpha_i \\
& = a_0b_0 + a_1b_1 + \big((a_0+a_1)(b_0+b_1) - a_0b_0 - a_1b_1) + a_1b_1\cdot\alpha_{i-1}\big)\cdot\alpha_i
\end{split} a ⋅ b = ( a 0 + a 1 ⋅ α i ) ⋅ ( b 0 + b 1 ⋅ α i ) = a 0 b 0 + ( a 0 b 1 + a 1 b 0 ) ⋅ α i + a 1 b 1 ⋅ α i 2 = a 0 b 0 + ( a 0 b 1 + a 1 b 0 ) ⋅ α i + a 1 b 1 ⋅ ( α i − 1 α i + 1 ) = a 0 b 0 + a 1 b 1 + ( a 0 b 1 + a 1 b 0 + a 1 b 1 ⋅ α i − 1 ) ⋅ α i = a 0 b 0 + a 1 b 1 + ( ( a 0 + a 1 ) ( b 0 + b 1 ) − a 0 b 0 − a 1 b 1 ) + a 1 b 1 ⋅ α i − 1 ) ⋅ α i 注意上面等式的右边,我们只需要计算三个 T i \mathcal{T}_{i} T i A = a 0 b 0 A=a_0b_0 A = a 0 b 0 B = ( a 0 + a 1 ) ( b 0 + b 1 ) B=(a_0+a_1)(b_0+b_1) B = ( a 0 + a 1 ) ( b 0 + b 1 ) C = a 1 b 1 C=a_1b_1 C = a 1 b 1
a ⋅ b = ( A + C ) + ( B − A − C + C ⋅ α i − 1 ) ⋅ α i a\cdot b = (A + C) + (B-A-C+C\cdot \alpha_{i-1})\cdot\alpha_i a ⋅ b = ( A + C ) + ( B − A − C + C ⋅ α i − 1 ) ⋅ α i 其中还漏了一个 C ⋅ α i − 1 C\cdot \alpha_{i-1} C ⋅ α i − 1 α i − 1 ∈ T i \alpha_{i-1}\in\mathcal{T}_{i} α i − 1 ∈ T i T i − 1 \mathcal{T}_{i-1} T i − 1
C ⋅ α i − 1 = ( c 0 + c 1 α i − 1 ) ⋅ α i − 1 = c 0 ⋅ α i − 1 + c 1 ⋅ α i − 1 2 = c 0 ⋅ α i − 1 + c 1 ⋅ ( α i − 2 ⋅ α i − 1 + 1 ) = c 1 + ( c 0 + c 1 ⋅ α i − 2 ) ⋅ α i − 1 \begin{split}
C\cdot \alpha_{i-1} &= (c_0 + c_1\alpha_{i-1})\cdot \alpha_{i-1} \\
& = c_0\cdot \alpha_{i-1} + c_1\cdot \alpha_{i-1}^2 \\
& = c_0\cdot \alpha_{i-1} + c_1\cdot (\alpha_{i-2}\cdot \alpha_{i-1} + 1) \\
& = c_1 + (c_0 + {\color{blue}c_1\cdot \alpha_{i-2}})\cdot \alpha_{i-1}
\end{split} C ⋅ α i − 1 = ( c 0 + c 1 α i − 1 ) ⋅ α i − 1 = c 0 ⋅ α i − 1 + c 1 ⋅ α i − 1 2 = c 0 ⋅ α i − 1 + c 1 ⋅ ( α i − 2 ⋅ α i − 1 + 1 ) = c 1 + ( c 0 + c 1 ⋅ α i − 2 ) ⋅ α i − 1 其中蓝色部分表达式,c 1 ⋅ α i − 2 {\color{blue}c_1\cdot \alpha_{i-2}} c 1 ⋅ α i − 2 T i − 2 \mathcal{T}_{i-2} T i − 2
再回头看看 a ⋅ b a\cdot b a ⋅ b
进一步,T i \mathcal{T}_{i} T i a , b ∈ T i + 1 a, b\in\mathcal{T}_{i+1} a , b ∈ T i + 1 a ⋅ b = 1 a\cdot b=1 a ⋅ b = 1 a a a b b b
a ⋅ b = ( a 0 + a 1 ⋅ α i ) ⋅ ( b 0 + b 1 ⋅ α i ) = a 0 b 0 + a 1 b 1 + ( ( a 0 + a 1 ) ( b 0 + b 1 ) − a 0 b 0 − a 1 b 1 ) + a 1 b 1 ⋅ α i − 1 ) ⋅ α i = 1 \begin{split}
a\cdot b &= (a_0 + a_1\cdot\alpha_i)\cdot (b_0 + b_1\cdot\alpha_i) \\
& = a_0b_0 + a_1b_1 + \big((a_0+a_1)(b_0+b_1) - a_0b_0 - a_1b_1) + a_1b_1\cdot\alpha_{i-1}\big)\cdot\alpha_i\\
&= 1\\
\end{split} a ⋅ b = ( a 0 + a 1 ⋅ α i ) ⋅ ( b 0 + b 1 ⋅ α i ) = a 0 b 0 + a 1 b 1 + ( ( a 0 + a 1 ) ( b 0 + b 1 ) − a 0 b 0 − a 1 b 1 ) + a 1 b 1 ⋅ α i − 1 ) ⋅ α i = 1 我们可以计算得到 b 0 , b 1 b_0, b_1 b 0 , b 1
b 0 = a 0 + a 1 α i − 1 a 0 ( a 0 + a 1 α i − 1 ) + a 1 2 b 1 = a 1 a 0 ( a 0 + a 1 α i − 1 ) + a 1 2 \begin{split}
b_0 &= \frac{a_0 + a_1\alpha_{i-1}}{a_0(a_0 + a_1\alpha_{i-1}) + a_1^2} \\[2ex]
b_1 &= \frac{a_1}{a_0(a_0 + a_1\alpha_{i-1}) + a_1^2} \\
\end{split} b 0 b 1 = a 0 ( a 0 + a 1 α i − 1 ) + a 1 2 a 0 + a 1 α i − 1 = a 0 ( a 0 + a 1 α i − 1 ) + a 1 2 a 1 所以,b 0 b_0 b 0 b 1 b_1 b 1
d 0 = α i − 1 a 1 d 1 = a 0 + d 0 d 2 = a 0 ⋅ d 1 d 3 = a 1 2 d 4 = d 2 + d 3 d 5 = 1 / d 4 b 0 = d 1 ⋅ d 5 b 1 = a 1 ⋅ d 5 \begin{split}
d_0 &= \alpha_{i-1}a_1\\
d_1 &= a_0 + d_0 \\
d_2 &= a_0 \cdot d_1 \\
d_3 &= a_1^2 \\
d_4 &= d_2 + d_3 \\
d_5 &= 1/d_4 \\
b_0 & = d_1\cdot d_5\\
b_1 & = a_1 \cdot d_5\\
\end{split} d 0 d 1 d 2 d 3 d 4 d 5 b 0 b 1 = α i − 1 a 1 = a 0 + d 0 = a 0 ⋅ d 1 = a 1 2 = d 2 + d 3 = 1/ d 4 = d 1 ⋅ d 5 = a 1 ⋅ d 5 其中 d 5 d_5 d 5 d 3 d_3 d 3
a 1 2 = ( e 0 + e 1 ⋅ α i − 1 ) 2 = e 0 2 + e 1 2 ⋅ α i − 1 2 = e 0 2 + e 1 2 ⋅ ( α i − 2 α i − 1 + 1 ) = ( e 0 2 + e 1 2 ) + ( e 1 2 α i − 2 ) ⋅ α i − 1 \begin{split}
a_1^2 &= (e_0 + e_1\cdot\alpha_{i-1})^2 \\
& = e_0^2 + e_1^2\cdot\alpha_{i-1}^2 \\
& = e_0^2 + e_1^2\cdot(\alpha_{i-2}\alpha_{i-1} + 1) \\
& = (e_0^2 + e_1^2) + (e_1^2\alpha_{i-2})\cdot\alpha_{i-1} \\
\end{split} a 1 2 = ( e 0 + e 1 ⋅ α i − 1 ) 2 = e 0 2 + e 1 2 ⋅ α i − 1 2 = e 0 2 + e 1 2 ⋅ ( α i − 2 α i − 1 + 1 ) = ( e 0 2 + e 1 2 ) + ( e 1 2 α i − 2 ) ⋅ α i − 1 详细的递归效率分析可以参考 [FP97]。总体上,这个计算复杂度和 Karatsuba 算法复杂度相当,从而很大程度上降低了求逆的算法复杂度。
Artin-Schreier Tower (Conway Tower) ¶ 还有一种构造 Binary Tower 的方法,源自 Amil Artin 与 Otto Schreier 发表在 1927 年的论文中,也出现在 Conway 的 「On Numbers and Games」一书中。关于这个历史溯源与相关理论,请参考 [CHS24]。
对于任意的 F p n \mathbb{F}_{p^n} F p n h ( X i + 1 ) = X i + 1 p − X i + 1 − α 0 α 1 ⋯ α i h(X_{i+1}) = X_{i+1}^p - X_{i+1} - \alpha_0\alpha_1\cdots \alpha_i h ( X i + 1 ) = X i + 1 p − X i + 1 − α 0 α 1 ⋯ α i α i + 1 \alpha_{i+1} α i + 1 h ( X i + 1 ) = 0 h(X_{i+1})=0 h ( X i + 1 ) = 0
F 2 ⊂ F 2 2 ≅ F 2 ( α 0 ) ⊂ F 2 4 ≅ F 2 2 ( α 1 ) ⊂ F 2 8 ≅ F 2 4 ( α 2 ) \mathbb{F}_2 \subset \mathbb{F}_{2^2}\cong\mathbb{F}_2(\alpha_0) \subset \mathbb{F}_{2^4}\cong\mathbb{F}_{2^2}(\alpha_1) \subset \mathbb{F}_{2^8}\cong\mathbb{F}_{2^4}(\alpha_2) F 2 ⊂ F 2 2 ≅ F 2 ( α 0 ) ⊂ F 2 4 ≅ F 2 2 ( α 1 ) ⊂ F 2 8 ≅ F 2 4 ( α 2 ) 而且 ( 1 , α 0 ) ⊗ ( 1 , α 1 ) ⊗ ⋯ ⊗ ( 1 , α n ) (1, \alpha_0)\otimes(1, \alpha_1)\otimes\cdots \otimes (1, \alpha_n) ( 1 , α 0 ) ⊗ ( 1 , α 1 ) ⊗ ⋯ ⊗ ( 1 , α n ) F 2 2 i + 1 \mathbb{F}_{2^{2^{i+1}}} F 2 2 i + 1
References ¶ [Wie88] Wiedemann, Doug. “An iterated quadratic extension of GF (2).” Fibonacci Quart 26.4 (1988): 290-295. [DP23] Diamond, Benjamin E., and Jim Posen. “Succinct arguments over towers of binary fields.” Cryptology ePrint Archive (2023). [DP24] Diamond, Benjamin E., and Jim Posen. “Polylogarithmic Proofs for Multilinears over Binary Towers.” Cryptology ePrint Archive (2024). [LN97] Lidl, Rudolf, and Harald Niederreiter. Finite fields. No. 20. Cambridge university press, 1997. [FP97] Fan, John L., and Christof Paar. “On efficient inversion in tower fields of characteristic two.” Proceedings of IEEE International Symposium on Information Theory. IEEE, 1997. [CHS24] Cagliero, Leandro, Allen Herman, and Fernando Szechtman. “Artin-Schreier towers of finite fields.” arXiv preprint arXiv:2405.10159 (2024). [Can89] David G. Cantor. On arithmetical algorithms over finite fields. J. Comb. Theory Ser. A, 50(2):285–300, March 1989.