Proof of Proximity ¶ 下面我们给出利用 Foldable code 来实现 IOPP 的证明。
假设有一个 MLE 多项式 f ~ ( X ) \tilde{f}(\mathbf{X}) f ~ ( X )
f ~ ( X 0 , X 1 , … , X d − 1 ) = f 0 + f 1 X 0 + f 2 X 1 + f 3 X 0 X 1 + ⋯ + f 2 d − 1 X d − 1 \tilde{f}(X_0, X_1, \ldots, X_{d-1}) = f_0 + f_1X_0 + f_2X_1 + f_3X_0X_1 + \cdots + f_{2^d-1}X_{d-1} f ~ ( X 0 , X 1 , … , X d − 1 ) = f 0 + f 1 X 0 + f 2 X 1 + f 3 X 0 X 1 + ⋯ + f 2 d − 1 X d − 1 由于 f ~ ( X ) \tilde{f}(X) f ~ ( X ) d d d 2 d 2^d 2 d
我们对 f ~ ( X ) \tilde{f}(\mathbf{X}) f ~ ( X ) f \mathbf{f} f c f = E n c ( f ) c_\mathbf{f}=\mathsf{Enc}(\mathbf{f}) c f = Enc ( f ) n d n_d n d
c m ( f ) = M e r k l i z e ( E n c ( f 0 , f 1 , f 2 , … , f 2 d − 1 ) ) \mathbf{cm}(\mathbf{f}) = \mathsf{Merklize}(\mathsf{Enc}(f_0, f_1, f_2, \ldots, f_{2^d-1})) cm ( f ) = Merklize ( Enc ( f 0 , f 1 , f 2 , … , f 2 d − 1 )) 与 FRI 协议类似,Basefold-IOPP 协议用来证明一个承诺 π d = c m ( f ) \pi_d=\mathbf{cm}(\mathbf{f}) π d = cm ( f ) C d C_d C d
Proof of Proximity 利用了线性编码的一个神奇性质:「Proximity Gap」,即如果两个向量 π , π ′ \pi, \pi' π , π ′ π + α ⋅ π ′ \pi+\alpha\cdot \pi' π + α ⋅ π ′
{ Δ ( π i , C i ) = 0 (with negligible probability) Δ ( π i , C i ) ≤ Δ ( π i + 1 , C i + 1 ) (with non-negligible probability) \begin{cases}
\Delta(\pi_{i}, C_i) = 0 & \text{(with negligible probability)} \\
\Delta(\pi_{i}, C_i) \leq \Delta(\pi_{i+1}, C_{i+1}) & \text{(with non-negligible probability)} \\
\end{cases} { Δ ( π i , C i ) = 0 Δ ( π i , C i ) ≤ Δ ( π i + 1 , C i + 1 ) (with negligible probability) (with non-negligible probability) 这就说明了对 codeword 的折叠过程不会破坏向量与合法 codeword space 之间的距离,这个把向量折叠到足够小之后,Verifier 可以用极小的代码来验证折叠最后产生的向量是否是合法 codeword,从而可以得知原始向量是否是合法 codeword。
📖 Notes on Proximity Gap
Proof of Proximity 利用了线性编码的一个神奇性质:「Proximity Gap」,即对两个向量 π , π ′ \pi, \pi' π , π ′ α ∈ F \alpha \in \mathbb{F} α ∈ F A = { π + α ⋅ π ′ : α ∈ F } A = \{\pi+\alpha\cdot \pi': \alpha \in \mathbb{F}\} A = { π + α ⋅ π ′ : α ∈ F } α \alpha α A A A C i C_{i} C i C i C_{i} C i C i C_{i} C i δ \delta δ
> Pr a ∈ A [ Δ ( a , C i ) ≤ δ ] = { > ϵ (small enough) > 1 > > > \Pr_{a \in A}[\Delta(a, C_{i}) \le \delta] = \begin{cases}
> \epsilon \quad \text{(small enough)}\\
> 1
> \end{cases}
> > a ∈ A Pr [ Δ ( a , C i ) ≤ δ ] = { > ϵ (small enough) > 1 > > 这样对于 Verifier 来说就可以大胆用随机数 α \alpha α π , π ′ \pi, \pi' π , π ′ C i C_{i} C i δ \delta δ C i C_{i} C i ϵ \epsilon ϵ π d \pi_{d} π d π 0 \pi_{0} π 0 π 0 \pi_{0} π 0 A = { π + α ⋅ π ′ : α ∈ F } A = \{\pi+\alpha\cdot \pi': \alpha \in \mathbb{F}\} A = { π + α ⋅ π ′ : α ∈ F }
Proof of Proximity 协议分为两个阶段:Commit-phase 和 Query-phase。前者的子协议是完成 codeword 的多次折叠过程,并产生每一次折叠后的 codeword 的承诺(或称为 Oracle);后者 Query-phase 是 Verifier 通过随机抽样来验证每一次的折叠过程是否合法。
Commit-phase ¶ 下面先解释下 Commit-phase。Prover 通过多次折叠编码 π d \pi_d π d n d n_d n d n d − 1 , … , n 0 n_{d-1}, \ldots, n_0 n d − 1 , … , n 0 ( π d − 1 , π d − 2 , … , π 0 ) (\pi_{d-1}, \pi_{d-2}, \ldots, \pi_0) ( π d − 1 , π d − 2 , … , π 0 ) d d d i i i 0 ≤ i < d 0 \leq i < d 0 ≤ i < d α i \alpha_{i} α i π i + 1 \pi_{i+1} π i + 1 π i \pi_{i} π i d d d n 0 n_0 n 0 π 0 \pi_0 π 0 ( π d , … , π 0 ) (\pi_d, \ldots, \pi_0) ( π d , … , π 0 ) c m ( π d ) , … , c m ( π 0 ) \mathsf{cm}(\pi_d), \ldots, \mathsf{cm}(\pi_0) cm ( π d ) , … , cm ( π 0 ) I O P P . C o m m i t \mathsf{IOPP.Commit} IOPP.Commit
下面我们分析下单次折叠 π i \pi_{i} π i π i ∈ C i \pi_{i}\in C_i π i ∈ C i π i = m G i \pi_{i}=\mathbf{m}G_i π i = m G i n i n_i n i
π i = ( c 0 , c 1 , c 2 , … , c n i − 1 ) \pi_i = (c_0, c_1, c_2, \ldots, c_{n_{i}-1}) π i = ( c 0 , c 1 , c 2 , … , c n i − 1 ) 我们把这个向量从中间拆分为两部分,上下叠放在一起:
( c 0 , c 1 , … , c n i − 1 − 1 c n i − 1 , c n i − 1 + 1 , … , c n i − 1 ) \left(
\begin{array}{cccc}
c_0, & c_1, & \ldots, & c_{n_{i-1}-1} \\
c_{n_{i-1}}, & c_{n_{i-1}+1}, & \ldots, & c_{n_{i}-1} \\
\end{array}
\right) ( c 0 , c n i − 1 , c 1 , c n i − 1 + 1 , … , … , c n i − 1 − 1 c n i − 1 ) 这时需要 Verifier 提供一个随机数 α ( i ) \alpha^{(i)} α ( i )
π i − 1 = ( f o l d α i ( c 0 , c n i − 1 ) , f o l d α i ( c 1 , c n i − 1 + 1 ) , … , f o l d α i ( c n i − 1 , c n i − 1 ) ) \pi_{i-1} = \big(\mathsf{fold}_{\alpha_i}(c_0, c_{n_{i-1}}), \mathsf{fold}_{\alpha_i}(c_1, c_{n_{i-1}+1}), \ldots, \mathsf{fold}_{\alpha_i}(c_{n_{i-1}}, c_{n_{i}-1})\big) π i − 1 = ( fold α i ( c 0 , c n i − 1 ) , fold α i ( c 1 , c n i − 1 + 1 ) , … , fold α i ( c n i − 1 , c n i − 1 ) ) 上面即为折叠后的向量 π i − 1 \pi_{i-1} π i − 1 C i − 1 C_{i-1} C i − 1 f o l d α i \mathsf{fold}_{\alpha_i} fold α i
f o l d α ( c j , c n i − 1 + j ) = t j ⋅ c n i − 1 + j − t j ′ ⋅ c j t j − t j ′ + α ⋅ ( c j − c n i − 1 + j ) t j − t j ′ \mathsf{fold}_{\alpha}(c_j, c_{n_{i-1}+j}) = \frac{t_j\cdot c_{n_{i-1}+j} - t'_j\cdot c_{j} }{t_j - t'_j} + \alpha\cdot \frac{(c_{j} - c_{n_{i-1}+j})}{t_j - t'_j} fold α ( c j , c n i − 1 + j ) = t j − t j ′ t j ⋅ c n i − 1 + j − t j ′ ⋅ c j + α ⋅ t j − t j ′ ( c j − c n i − 1 + j ) 如何理解上面的 f o l d α ( ⋅ , ⋅ ) \mathsf{fold}_{\alpha}(\cdot, \cdot) fold α ( ⋅ , ⋅ ) d i a g ( T i ) = ( t 0 , t 1 , … , t n i − 1 − 1 ) \mathsf{diag}(T_i)=(t_0, t_1, \ldots, t_{n_{i-1}-1}) diag ( T i ) = ( t 0 , t 1 , … , t n i − 1 − 1 ) d i a g ( T i ′ ) = ( t 0 ′ , t 1 ′ , … , t n i − 1 − 1 ′ ) \mathsf{diag}(T'_i)=(t'_0, t'_1, \ldots, t'_{n_{i-1}-1}) diag ( T i ′ ) = ( t 0 ′ , t 1 ′ , … , t n i − 1 − 1 ′ )
( ( t 0 , c 0 ) , ( t 1 , c 1 ) , … , ( t i − 1 , c n i − 1 − 1 ) ( t 0 ′ , c n i − 1 ) , ( t 1 ′ , c n i − 1 + 1 ) , … , ( t i − 1 ′ , c n i − 1 ) ) \left(
\begin{array}{cccc}
(t_0, c_0), & (t_1, c_1), & \ldots, & (t_{i-1}, c_{n_{i-1}-1}) \\
(t'_0, c_{n_{i-1}}), & (t'_1, c_{n_{i-1}+1}), & \ldots, & (t'_{i-1}, c_{n_{i}-1}) \\
\end{array}
\right) ( ( t 0 , c 0 ) , ( t 0 ′ , c n i − 1 ) , ( t 1 , c 1 ) , ( t 1 ′ , c n i − 1 + 1 ) , … , … , ( t i − 1 , c n i − 1 − 1 ) ( t i − 1 ′ , c n i − 1 ) ) 然后我们对上面矩阵的每一列在 Domain ( t j , t j ′ ) (t_j, t'_j) ( t j , t j ′ ) n i − 1 = n i / 2 n_{i-1}={n_i}/{2} n i − 1 = n i / 2 p j ( i − 1 ) ( X ) p^{(i-1)}_j(X) p j ( i − 1 ) ( X ) 0 ≤ j < n i − 1 0\leq j < n_{i-1} 0 ≤ j < n i − 1 p j ( i − 1 ) ( X ) p^{(i-1)}_j(X) p j ( i − 1 ) ( X ) X = α i X=\alpha_{i} X = α i n i − 1 n_{i-1} n i − 1 X = α i X=\alpha_{i} X = α i π i − 1 \pi_{i-1} π i − 1
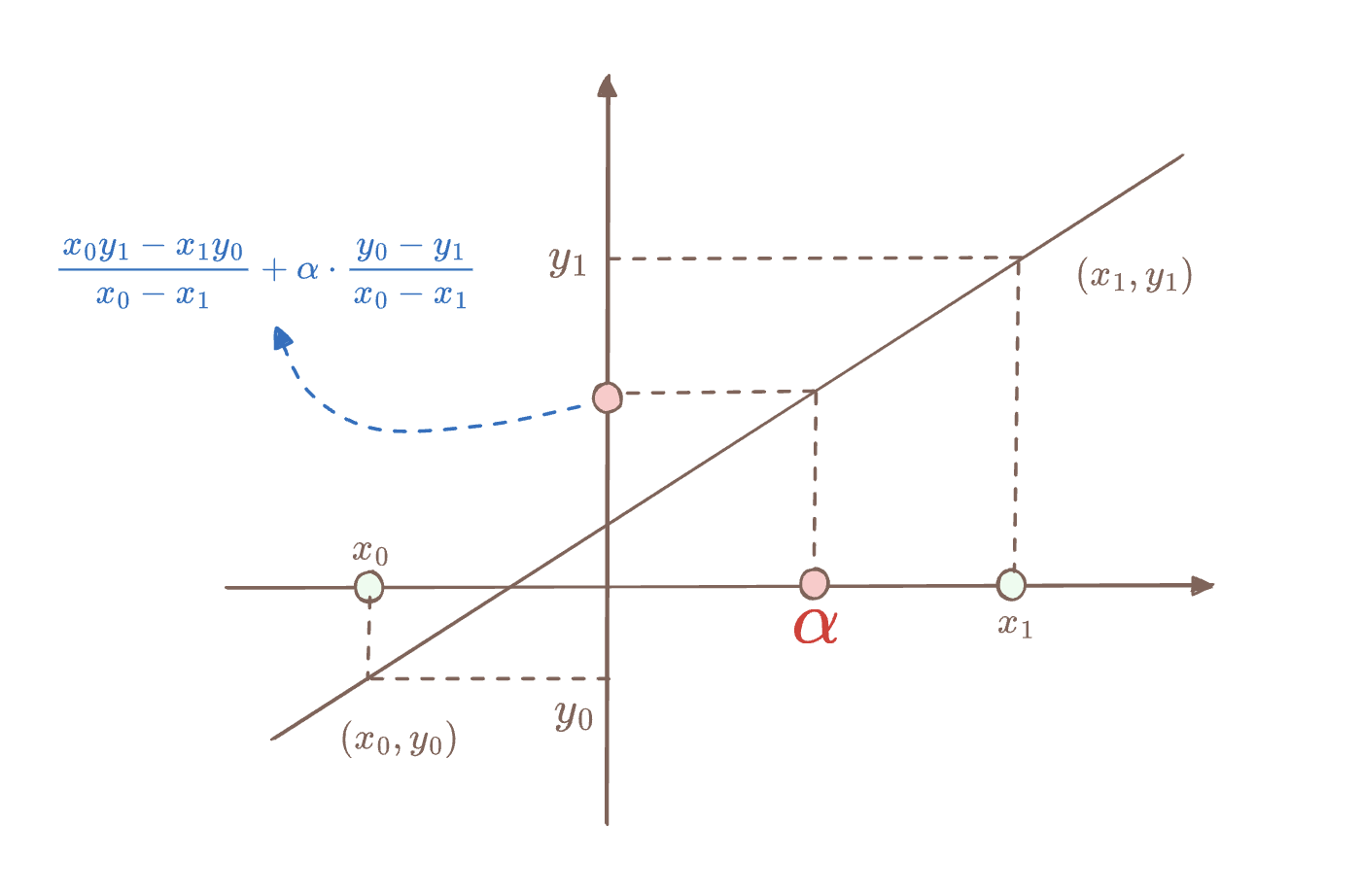
这里折叠函数的定义和线性多项式插值过程应该是一致的,我们可以手动推导一下折叠函数的定义的由来。因为这里我们对 π i \pi_{i} π i n i − 1 n_{i-1} n i − 1 j j j ( x 0 , y 0 ) , ( x 1 , y 1 ) (x_0, y_0), (x_1, y_1) ( x 0 , y 0 ) , ( x 1 , y 1 ) p ( X ) p(X) p ( X )
p ( X ) = y 0 x 0 − x 1 ( X − x 1 ) + y 1 x 1 − x 0 ( X − x 0 ) = x 0 y 1 − x 1 y 0 x 0 − x 1 + y 0 − y 1 x 0 − x 1 ⋅ X \begin{split}
p(X) &= \frac{y_0}{x_0-x_1}(X-x_1) + \frac{y_1}{x_1-x_0}(X-x_0) \\[2ex]
&= \frac{x_0y_1-x_1y_0}{x_0-x_1} + \frac{y_0-y_1}{x_0-x_1}\cdot X
\end{split} p ( X ) = x 0 − x 1 y 0 ( X − x 1 ) + x 1 − x 0 y 1 ( X − x 0 ) = x 0 − x 1 x 0 y 1 − x 1 y 0 + x 0 − x 1 y 0 − y 1 ⋅ X x 0 = t j , x 1 = t j ′ x_0=t_j, x_1=t'_j x 0 = t j , x 1 = t j ′ X = α X=\alpha X = α f o l d α ( y 0 , y 1 ) \mathsf{fold}_\alpha(y_0, y_1) fold α ( y 0 , y 1 )
f o l d α ( y 0 , y 1 ) = p ( α ) = t j ⋅ y 1 − t j ′ ⋅ y 0 t j − t j ′ + y 0 − y 1 t j − t j ′ ⋅ α \begin{split}
\mathsf{fold}_\alpha(y_0, y_1) = p(\alpha) &= \frac{t_j\cdot y_1 - t'_j\cdot y_0}{t_j - t'_j} + \frac{y_0-y_1}{t_j - t'_j}\cdot \alpha\\
\end{split} fold α ( y 0 , y 1 ) = p ( α ) = t j − t j ′ t j ⋅ y 1 − t j ′ ⋅ y 0 + t j − t j ′ y 0 − y 1 ⋅ α 如果 x 0 x_0 x 0 x 1 x_1 x 1 t j = − t j ′ t_j=-t'_j t j = − t j ′ f o l d α ( y 0 , y 1 ) \mathsf{fold}_\alpha(y_0, y_1) fold α ( y 0 , y 1 )
f o l d α ( y 0 , y 1 ) = 1 2 ( y 0 + y 1 ) + α ⋅ y 0 − y 1 2 ⋅ t j \mathsf{fold}_\alpha(y_0, y_1) = \frac{1}{2}(y_0 + y_1) + \alpha\cdot \frac{y_0-y_1}{2\cdot t_j} fold α ( y 0 , y 1 ) = 2 1 ( y 0 + y 1 ) + α ⋅ 2 ⋅ t j y 0 − y 1 因为我们用折叠函数定义了折叠后 codeword c ( i − 1 ) \mathbf{c}^{(i-1)} c ( i − 1 ) G i − 1 G_{i-1} G i − 1 i i i c ( i ) \mathbf{c}^{(i)} c ( i ) m \mathbf{m} m
π i = m G i = ( m l ∥ m r ) [ G i − 1 G i − 1 G i − 1 ⋅ T i − 1 G i − 1 ⋅ T i − 1 ′ ] = ( m l G i − 1 + m r G i − 1 ∘ d i a g ( T i − 1 ) ) ∥ ( m l G i − 1 + m r G i − 1 ∘ d i a g ( T i − 1 ′ ) ) \begin{split}
\pi_{i} &= \mathbf{m} G_i \\
& = (\mathbf{m}_l \parallel \mathbf{m}_r)\begin{bmatrix}
G_{i-1} & G_{i-1} \\
G_{i-1}\cdot T_{i-1} & G_{i-1}\cdot T'_{i-1}
\end{bmatrix}\\[4ex]
&=\Big(\mathbf{m}_l G_{i-1} + \mathbf{m}_r G_{i-1}\circ \mathbf{diag}(T_{i-1})\Big) \parallel \Big(\mathbf{m}_l G_{i-1} + \mathbf{m}_r G_{i-1}\circ \mathbf{diag}(T'_{i-1})\Big)\\
\end{split} π i = m G i = ( m l ∥ m r ) [ G i − 1 G i − 1 ⋅ T i − 1 G i − 1 G i − 1 ⋅ T i − 1 ′ ] = ( m l G i − 1 + m r G i − 1 ∘ diag ( T i − 1 ) ) ∥ ( m l G i − 1 + m r G i − 1 ∘ diag ( T i − 1 ′ ) ) 而 Prover 将其对半折叠后,得到的新的 codeword 为:
f o l d α ( π i ) = ( f o l d α ( π i [ 0 ] , π i [ n i − 1 ] ) , f o l d α ( π i [ 1 ] , π i [ n i − 1 + 1 ] ) , … , f o l d α ( π i [ n i − 1 − 1 ] , π i [ n i − 1 ] ) ) \begin{split}
\mathsf{fold}_\alpha(\pi_{i}) &= \Big(\mathsf{fold}_\alpha(\pi_{i}[0], \pi_{i}[n_{i-1}]), \mathsf{fold}_\alpha(\pi_{i}[1], \pi_{i}[n_{i-1}+1]), \ldots, \mathsf{fold}_\alpha(\pi_{i}[n_{i-1}-1], \pi_{i}[n_{i}-1])\Big) \\
\end{split} fold α ( π i ) = ( fold α ( π i [ 0 ] , π i [ n i − 1 ]) , fold α ( π i [ 1 ] , π i [ n i − 1 + 1 ]) , … , fold α ( π i [ n i − 1 − 1 ] , π i [ n i − 1 ]) ) 我们现在验证其中每一个 f o l d α ( π i [ j ] , π i [ n i − 1 + j ] ) \mathsf{fold}_\alpha(\pi_{i}[j], \pi_{i}[n_{i-1}+j]) fold α ( π i [ j ] , π i [ n i − 1 + j ]) m l G i − 1 [ j ] \mathbf{m}_lG_{i-1}[j] m l G i − 1 [ j ] m r G i − 1 [ j ] \mathbf{m}_rG_{i-1}[j] m r G i − 1 [ j ] α \alpha α
f o l d α ( π i [ j ] , π i [ n i − 1 + j ] ) = 1 t j − t j ′ ⋅ ( t j ⋅ ( m l G i − 1 [ j ] + t j ′ ⋅ m r G i − 1 [ j ] ) − t j ′ ⋅ ( m l G i − 1 [ j ] + t j ⋅ m r G i − 1 [ j ] ) ) + α t j − t j ′ ⋅ ( m l G i − 1 [ j ] + t j ⋅ m r G i − 1 [ j ] − m l G i − 1 [ j ] − t j ′ ⋅ m r G i − 1 [ j ] ) = m l G i − 1 [ j ] + α ⋅ m r G i − 1 [ j ] \begin{split}
\mathsf{fold}_\alpha(\pi_{i}[j], \pi_{i}[n_{i-1}+j]) & = \frac{1}{t_j - t'_j}\cdot\Big(
t_j\cdot (\mathbf{m}_l G_{i-1}[j] + t'_j\cdot \mathbf{m}_r G_{i-1}[j]) - t'_j\cdot(\mathbf{m}_l G_{i-1}[j] + t_j\cdot \mathbf{m}_r G_{i-1}[j]) \Big)\\
& + \frac{\alpha}{t_j - t'_j}\cdot \Big(\mathbf{m}_l G_{i-1}[j] + t_j\cdot \mathbf{m}_r G_{i-1}[j] - \mathbf{m}_l G_{i-1}[j] - t'_j\cdot \mathbf{m}_r G_{i-1}[j] \Big) \\
& = \mathbf{m}_l G_{i-1}[j] + \alpha\cdot \mathbf{m}_r G_{i-1}[j]
\end{split} fold α ( π i [ j ] , π i [ n i − 1 + j ]) = t j − t j ′ 1 ⋅ ( t j ⋅ ( m l G i − 1 [ j ] + t j ′ ⋅ m r G i − 1 [ j ]) − t j ′ ⋅ ( m l G i − 1 [ j ] + t j ⋅ m r G i − 1 [ j ]) ) + t j − t j ′ α ⋅ ( m l G i − 1 [ j ] + t j ⋅ m r G i − 1 [ j ] − m l G i − 1 [ j ] − t j ′ ⋅ m r G i − 1 [ j ] ) = m l G i − 1 [ j ] + α ⋅ m r G i − 1 [ j ] 于是,整个 π i \pi_{i} π i m l G i − 1 \mathbf{m}_lG_{i-1} m l G i − 1 m r G i − 1 \mathbf{m}_rG_{i-1} m r G i − 1 α \alpha α
f o l d α ( π i ) = m l G i − 1 + α ⋅ m r G i − 1 = ( m l + α ⋅ m r ) G i − 1 \mathsf{fold}_\alpha(\pi_{i}) = \mathbf{m}_l G_{i-1} + \alpha\cdot \mathbf{m}_r G_{i-1} = (\mathbf{m}_l + \alpha\cdot \mathbf{m}_r)G_{i-1} fold α ( π i ) = m l G i − 1 + α ⋅ m r G i − 1 = ( m l + α ⋅ m r ) G i − 1 折叠后的 codeword 恰好是 m \mathbf{m} m α \alpha α m ( i − 1 ) \mathbf{m}^{(i-1)} m ( i − 1 ) G i − 1 G_{i-1} G i − 1 π i − 1 \pi_{i-1} π i − 1 T i T_i T i T i ′ T'_i T i ′
下面我们用一个简单的例子来走一遍协议的流程,来看看 Basefold-IOPP 协议的 Commit-phase 是如何运作的。
公共输入
MLE 多项式 f ~ \tilde{f} f ~ π 3 = E n c 3 ( f ) = f G 3 \pi_3=\mathsf{Enc}_3(\mathbf{f})=\mathbf{f}G_3 π 3 = Enc 3 ( f ) = f G 3 Witness
MLE 多项式 f ~ \tilde{f} f ~ f = ( f 0 , f 1 , f 2 , f 3 , f 4 , f 5 , f 6 , f 7 ) \mathbf{f} = (f_0, f_1, f_2, f_3, f_4, f_5, f_6, f_7) f = ( f 0 , f 1 , f 2 , f 3 , f 4 , f 5 , f 6 , f 7 ) 第一轮:Verifier 发送随机数 α 2 \alpha_2 α 2
第二轮:Prover 计算 π 2 = f o l d α ( π 3 ) \pi_2 = \mathsf{fold}_\alpha(\pi_3) π 2 = fold α ( π 3 )
计算 π 2 \pi_2 π 2
π 2 [ j ] = f o l d α ( π 3 [ j ] , π 3 [ j + 4 ] ) , j ∈ { 0 , 1 , 2 , 3 } \pi_2[j] = \mathsf{fold}_\alpha(\pi_3[j], \pi_3[j+4]), \quad j\in\{0, 1, 2, 3\} π 2 [ j ] = fold α ( π 3 [ j ] , π 3 [ j + 4 ]) , j ∈ { 0 , 1 , 2 , 3 } 计算出的 π 2 = E n c 2 ( f ( 2 ) ) \pi_2 = \mathsf{Enc}_2(f^{(2)}) π 2 = Enc 2 ( f ( 2 ) ) π 2 \pi_2 π 2 f ( 2 ) f^{(2)} f ( 2 ) f ( 2 ) f^{(2)} f ( 2 ) f f f α 2 \alpha_2 α 2
f ( 2 ) ( X 0 , X 1 ) = f ( X 0 , X 1 , α 2 ) = ( f 0 + f 4 α 2 ) + ( f 1 + f 5 α 2 ) X 0 + ( f 2 + f 6 α 2 ) X 1 + ( f 3 + f 7 α 2 ) X 0 X 1 f^{(2)}(X_0, X_1) = f(X_0, X_1, \alpha_2) = (f_0 + f_4\alpha_2) + (f_1 + f_5\alpha_2)X_0 + (f_2 + f_6\alpha_2)X_1 + (f_3 + f_7\alpha_2)X_0X_1 f ( 2 ) ( X 0 , X 1 ) = f ( X 0 , X 1 , α 2 ) = ( f 0 + f 4 α 2 ) + ( f 1 + f 5 α 2 ) X 0 + ( f 2 + f 6 α 2 ) X 1 + ( f 3 + f 7 α 2 ) X 0 X 1 第三轮:Verifier 发送随机数 α 1 \alpha_1 α 1
第四轮:Prover 计算 π 1 = f o l d α ( π 2 ) \pi_1 = \mathsf{fold}_\alpha(\pi_2) π 1 = fold α ( π 2 )
计算 π 1 \pi_1 π 1
π 1 [ j ] = f o l d α ( π 2 [ j ] , π 2 [ j + 2 ] ) , j ∈ { 0 , 1 } \pi_1[j] = \mathsf{fold}_\alpha(\pi_2[j], \pi_2[j+2]), \quad j\in\{0, 1\} π 1 [ j ] = fold α ( π 2 [ j ] , π 2 [ j + 2 ]) , j ∈ { 0 , 1 } 计算出的 π 1 = E n c 1 ( f ( 1 ) ) \pi_1 = \mathsf{Enc}_1(f^{(1)}) π 1 = Enc 1 ( f ( 1 ) ) π 1 \pi_1 π 1 f ( 1 ) f^{(1)} f ( 1 ) f ( 1 ) f^{(1)} f ( 1 ) f ( 2 ) f^{(2)} f ( 2 ) α 1 \alpha_1 α 1
f ( 1 ) ( X 0 ) = f ( X 0 , α 1 , α 2 ) = ( f 0 + f 4 α 2 + α 1 ( f 2 + + f 6 α 2 ) ) + ( f 1 + f 5 α 2 + α 1 ( f 3 + + f 7 α 2 ) ) X 0 f^{(1)}(X_0) = f(X_0, \alpha_1, \alpha_2) = (f_0 + f_4 \alpha_2 + \alpha_1 (f_2 + + f_6 \alpha_2)) + (f_1 + f_5 \alpha_2 + \alpha_1 (f_3 + + f_7 \alpha_2))X_0 f ( 1 ) ( X 0 ) = f ( X 0 , α 1 , α 2 ) = ( f 0 + f 4 α 2 + α 1 ( f 2 + + f 6 α 2 )) + ( f 1 + f 5 α 2 + α 1 ( f 3 + + f 7 α 2 )) X 0 第五轮:Verifier 发送随机数 α 0 \alpha_0 α 0
第六轮:Prover 计算 π 0 = f o l d α ( π 1 ) \pi_0 = \mathsf{fold}_\alpha(\pi_1) π 0 = fold α ( π 1 )
计算 π 0 \pi_0 π 0
π 0 [ j ] = f o l d α ( π 1 [ j ] , π 1 [ j + 1 ] ) , j = 0 \pi_0[j] = \mathsf{fold}_\alpha(\pi_1[j], \pi_1[j+1]), \quad j=0 π 0 [ j ] = fold α ( π 1 [ j ] , π 1 [ j + 1 ]) , j = 0 同样 π 0 = E n c 0 ( f ( 0 ) ) \pi_0 = \mathsf{Enc}_0(f^{(0)}) π 0 = Enc 0 ( f ( 0 ) ) π 0 \pi_0 π 0 f ( 0 ) f^{(0)} f ( 0 ) f ( 0 ) f^{(0)} f ( 0 ) f f f ( α 0 , α 1 , α 2 ) (\alpha_0, \alpha_1, \alpha_2) ( α 0 , α 1 , α 2 )
f ( 0 ) = f ( α 0 , α 1 , α 2 ) = f 0 + f 1 α 0 + f 2 α 1 + f 3 α 0 α 1 + f 4 α 2 + f 5 α 0 α 2 + f 6 α 1 α 2 + f 7 α 0 α 1 α 2 f^{(0)} = f(\alpha_0, \alpha_1, \alpha_2) = f_0 + f_1\alpha_0 + f_2\alpha_1 + f_3\alpha_0 \alpha_1 + f_4\alpha_2 + f_5\alpha_0\alpha_2 + f_6\alpha_1\alpha_2 + f_7\alpha_0\alpha_1\alpha_2 f ( 0 ) = f ( α 0 , α 1 , α 2 ) = f 0 + f 1 α 0 + f 2 α 1 + f 3 α 0 α 1 + f 4 α 2 + f 5 α 0 α 2 + f 6 α 1 α 2 + f 7 α 0 α 1 α 2 到此,Commit-phase 结束,Prover 总共发送了 ( π 2 , π 1 , π 0 ) (\pi_{2}, \pi_{1}, \pi_0) ( π 2 , π 1 , π 0 ) π 0 \pi_0 π 0 π i \pi_i π i π i \pi_i π i
Query-phase ¶ 与 FRI 协议类似,在 Query-phase 阶段,Verifier 要对 Prover 发送的 ( π d , π d − 1 , … , π 0 ) (\pi_{d}, \pi_{d-1}, \ldots, \pi_0) ( π d , π d − 1 , … , π 0 )
Verifier 会在 π d \pi_{d} π d μ \mu μ 0 ≤ μ < n d − 1 0\leq \mu < n_{d-1} 0 ≤ μ < n d − 1 n d − 1 n_{d-1} n d − 1 π d \pi_{d} π d π d [ μ ] \pi_{d}[\mu] π d [ μ ] π d [ μ + n d − 1 ] \pi_{d}[\mu+n_{d-1}] π d [ μ + n d − 1 ] π d − 1 \pi_{d-1} π d − 1 μ \mu μ π d − 1 [ μ ] \pi_{d-1}[\mu] π d − 1 [ μ ]
Verifier 收到后,首先验证这三个点是否对应到 π d \pi_{d} π d π d − 1 \pi_{d-1} π d − 1
π d − 1 [ μ ] = ? f o l d α d − 1 ( π d [ μ ] , π d [ μ + n d − 1 ] ) \pi_{d-1}[\mu] \overset{?}{=} \mathsf{fold}_{\alpha_{d-1}}(\pi_{d}[\mu], \pi_{d}[\mu+n_{d-1}]) π d − 1 [ μ ] = ? fold α d − 1 ( π d [ μ ] , π d [ μ + n d − 1 ]) 只验证 π d \pi_d π d π d − 1 \pi_{d-1} π d − 1 π d − 1 \pi_{d-1} π d − 1 π 0 \pi_{0} π 0 π d − 1 \pi_{d-1} π d − 1 π d − 2 \pi_{d-2} π d − 2 μ \mu μ π d − 1 [ μ ] \pi_{d-1}[\mu] π d − 1 [ μ ] α d − 2 \alpha_{d-2} α d − 2 μ < n d − 2 \mu < n_{d-2} μ < n d − 2 π d − 1 [ μ + n d − 2 ] \pi_{d-1}[\mu+n_{d-2}] π d − 1 [ μ + n d − 2 ] μ ≥ n d − 2 \mu \geq n_{d-2} μ ≥ n d − 2 π d − 1 [ μ − n d − 2 ] \pi_{d-1}[\mu-n_{d-2}] π d − 1 [ μ − n d − 2 ] μ ≥ n d − 2 \mu \geq n_{d-2} μ ≥ n d − 2 π d − 1 [ μ − n d − 2 ] \pi_{d-1}[\mu-n_{d-2}] π d − 1 [ μ − n d − 2 ] π d − 1 \pi_{d-1} π d − 1 π d − 2 \pi_{d-2} π d − 2
这样一来,Verifier 只需要给一个随机数 μ \mu μ π d \pi_{d} π d π 0 \pi_{0} π 0
为了将可靠性提升到一个足够的高度,Verifier 要进行多轮,确保 Prover 没有作弊空间。Query-phase 正是利用了 Proximity Gap 这一特性。Prover 篡改后的 codeword 大概率距离合法的编码空间比较远,这样 Verifier 只需要少量的抽样次数即可发现作弊行为。
本文描述了下 Basefold-IOPP 协议的 Commit-phase 和 Query-phase 的框架。这个框架是对 FRI 协议的一个泛化和扩展,从 RS-Code 扩展到了任何的 Foldable Linear Codes。但是请注意,Basefold 并不支持 Degree 大于 2 的 codeword 折叠。这样由于 Basefold-IOPP 协议不仅仅要完成 Proximity Testing,还要提供一个 MLE 多项式的运算结果。这将是本系列文章的下一篇。
References ¶ [ZCF23] Hadas Zeilberger, Binyi Chen, and Ben Fisch. “BaseFold: efficient field-agnostic polynomial commitment schemes from foldable codes.” Annual International Cryptology Conference. Cham: Springer Nature Switzerland, 2024. [BCIKS20] Eli Ben-Sasson, Dan Carmon, Yuval Ishai, Swastik Kopparty, and Shubhangi Saraf. Proximity Gaps for Reed–Solomon Codes. In Proceedings of the 61st Annual IEEE Symposium on Foundations of Computer Science , pages 900–909, 2020.
 代入 ,还有 我们即可得到上面折叠函数 的定义
代入 ,还有 我们即可得到上面折叠函数 的定义