ZeroMorph 笔记

• Yu Guo yu.guo@secbit.io

Zeromorph [KT23] 是一个基于 KZG10 的 MLE 多项式承诺方案。事实上，Zeromorph 方案是一个更一般性的框架，可以基于不同的 Univariate Polynomial Commitment 方案，比如 FRI-based Zeromorph 方案。

Zeromorph 的核心要点是将 MLE 多项式的 Evaluations 即「点值向量」作为 Univariate 多项式的「系数向量」。这个做法看起来有些奇怪，不过这个框架仍然不失清晰简洁性。

理解 Zeromorph 的关键在于对高维的 Boolean Hypercube 上取值的变换的理解，以及它们如何对应于 Univariate 多项式的运算。

MLE 多项式

所谓的 MLE（Multilinear Extension） 多项式 \(\tilde{f}\) 是定义在 Boolean Hypercube 上的一类 Multivariate 多项式。它的每一项中任何一个未知数的次数都不超过 \(1\)，例如 \(\tilde{f}=1 + 2X_0 + 3X_1X_0\) 是一个 MLE 多项式，而 \(\tilde{f}'=1 + 2X_0^2 + 3X_1X_0 + X_1\) 则不是，因为 \(X_0^2\) 的次数大于 \(1\)。

一个 MLE 多项式可以对应到一个从 Boolean 向量到一个有限域的函数，即 \(f:\{0,1\}^n\to \mathbb{F}_q\)，我们则称其维度为 \(n\) 。下图是一个三维的 MLE 多项式 \(\tilde{f}(X_0, X_1, X_2)\) 的示例，这个多项式可以唯一地被 \((a_0, a_1, \ldots, a_7)\) 这个「点值向量」来表示。这对应于 Univariate 多项式中的「点值式」表示，即 Evaluations form。

当然一个 MLE 多项式也可以采用「系数式」来表示，即 Coefficients form ，表示如下：

\[ \tilde{f}(X_0, X_1, \ldots, X_{n-1}) = \sum_{i_0=0}^{1}\sum_{i_1=0}^{1}\cdots \sum_{i_{n-1}=0}^{1} f_{i_0i_1\cdots i_{n-1}} X_0^{i_0}X_1^{i_1}\cdots X_{n-1}^{i_{n-1}} \]

对于上图三维 MLE 多项式的例子，我们可以将它写为：

\[ \tilde{f}(X_0, X_1, X_2) = f_0 + f_1X_0 + f_2X_1 + f_3X_2 + f_4X_0X_1 + f_5X_0X_2 + f_6X_1X_2 + f_7X_0X_1X_2 \]

其中 \((f_0, f_1, \ldots, f_7)\) 为 MLE 多项式的系数向量。注意因为 MLE 多项式属于多元多项式（Multivariate Polynomial），任何表示方式都需要事先确定多项式中的项的排序顺序，本文以及后续讨论我们都基于 Lexicographic Order。

对于 MLE 多项式的「点值式」表示，我们可以定义为：

\[ \tilde{f}(X_0, X_1, \ldots, X_{n-1}) = \sum_{i_0=0}^{1}\sum_{i_1=0}^{1}\cdots \sum_{i_{n-1}=0}^{1} a_{i_0i_1\cdots i_{n-1}}\cdot eq(i_0, i_1, \ldots, i_{n-1}, X_0, X_1, \ldots, X_{n-1}) \]

其中 \(eq\) 为 一组关于 \(n\) 维 Boolean Hypercube \(\{0, 1\}^n\) 的 Lagrange Polynomial：

\[ eq(i_0, i_1, \ldots, i_{n-1}, X_0, X_1, \ldots, X_{n-1}) = \prod_{j=0}^{n-1} \Big((1-i_j)\cdot (1-X_j)+ i_j\cdot X_j\Big) \]

MLE 多项式在「点值式」和「系数式」之间存在 \(N\log(N)\) 的转换算法，这里不再深入讨论。

我们可以使用 ZeroMorph 将一个 MLE 多项式映射到一个 Univariate 多项式，具体一点说，是将 MLE 多项式在 Boolean Hypercube 上的「点值向量」映射到一个 Univariate 多项式 的「系数向量」。

MLE 多项式到 Univariate 多项式

我们以一个简单的例子来快速了解下这个映射关系。考虑下面一个维度只有 2 的 MLE 多项式：

\[ \tilde{f}(X_0, X_1) = 2 + X_1 + X_0X_1 \]

容易验证，它在 Boolean Hypercube 上的点值表示为：

\[\begin{split} \begin{split} \tilde{f}(0,0) = 2 \\ \tilde{f}(1,0) = 2 \\ \tilde{f}(0,1) = 3 \\ \tilde{f}(1,1) = 4 \\ \end{split} \end{split}\]

如果采用 ZeroMorph 方案，它可以映射到如下的 Univariate 多项式：

\[ \hat{f}(X) = 2 + 2\cdot X + 3\cdot X^2 + 4\cdot X^3 \]

假设我们有一个 Univariate 多项式的承诺方案，那么我们就可以计算映射后的 Univariate 多项式的承诺。例如，假设我们有以下的 KZG10 承诺方案的 SRS：

\[ SRS = ([1]_1, [\tau]_1, [\tau^2]_1, [\tau^3]_1, \ldots, [\tau^{D}]_1, [1]_2, [\tau]_2, [\tau^2]_2, [\tau^3]_2, \ldots, [\tau^D]_2) \]

根据 KZG10 的承诺算法，我们计算 \(\hat{f}(X)\) 的承诺如下：

\[ \mathsf{cm}(\hat{f}) = 2\cdot [1]_1 + 2\cdot [\tau]_1 + 3\cdot [\tau^2]_1 + 4\cdot [\tau^3]_1 \]

后续我们用符号 \([[\tilde{f}]]\) 来表示 MLE 多项式 \(\tilde{f}\) 映射所对应的 Univariate 多项式。

多项式映射

这一节，我们讨论下更多的映射情况。为了简化起见，我们先考虑三维 MLE 的情况，即 \(\tilde{f}\in \mathbb{F}_q[X_0, X_1, X_2]^{\leq 1}\)。

假设 \(\tilde{f}\) 只是一个常数多项式，即它的系数向量只有第一项非零，其余元素都为零。多项式可以表示如下：

\[ \tilde{c}(X_0, X_1, X_2) = c_0 \]

我们考虑下这样一个常数多项式会映射到一个什么样的 Univariate 多项式。首先我们要把它转换成点值式，考虑在一个三维的 Boolean Hypercube 上，无论 \(X_0,X_1,X_2\in\{0, 1\}\) 如何取值，这个多项式在 Boolean Hypercube 上的取值都为 \(c_0\)，那么这也意味着它的点值式为 \((c_0, c_0, c_0, \ldots, c_0)\)，于是它所对应的 Univariate 多项式为：

\[\begin{split} \begin{split} [[\tilde{c}]] &= c_0 + c_0X + c_0X^2 + c_0X^3 + \ldots + c_0X^{7} \\ & = c_0 \cdot (1 + X + X^2 + X^3 + \ldots + X^{7}) \\ \end{split} \end{split}\]

那我们再考虑一个二维的 MLE 多项式 \(\tilde{c}'(X_0, X_1)\)，它同样是一个常数多项式，即 \(\tilde{c}'(X_0, X_1) = c_0\)，那么它对应的 Univariate 多项式为：

\[\begin{split} \begin{split} [[\tilde{c}']] &= c_0 + c_0X + c_0X^2 + c_0X^3 \\ & = c_0 \cdot (1 + X + X^2 + X^3) \\ \end{split} \end{split}\]

我们可以看到，虽然两个 MLE 多项式 \(\tilde{c}\) 和 \(\tilde{c}'\) 的系数式表示完全一样，但它们映射到的 Univariate 多项式并不一样。这是因为不管是 Univariate 还是 Multivariate 的多项式，它们的点值式表示都隐含了 Evaluation Domain 的选取。\(\tilde{c}\) 的 Evaluation Domain 是 3 维的 Boolean Hypercube，而 \(\tilde{c}'\) 的 Evaluation Domain 是 2 维的 Boolean Hypercube。因此，当我们计算多项式的点值式时，需要明确下 Evaluation Domain 的选择，对于 MLE 多项式来说，如果它的 Evaluation Domain 是 \(n\) 维的 Boolean Hypercube，那么我们修改下映射记号表示，在映射括加上下标 \(n\)，即 \([[\tilde{f}]]_n\) 。下面是 \(\tilde{c}\) 在两个不同的 Evaluation Domain 上的映射所产生的两个不同的 Univariate 多项式：

\[\begin{split} \begin{split} [[\tilde{c}]]_2 &= c_0 + c_0X + c_0X^2 + c_0X^3 \\ [[\tilde{c}]]_3 &= c_0 + c_0X + c_0X^2 + c_0X^3 + c_0X^4 + c_0X^5 + c_0X^6 + c_0X^7 \\ \end{split} \end{split}\]

映射的加法同态

对于任意两个维度相同的 MLE 多项式，比如 \(\tilde{f}_1(X_0, X_1)\) 和 \(\tilde{f}_2(X_0, X_1)\) ，假如两者的点值式表示为

\[ \tilde{f}_1(X_0, X_1) = v_0\cdot eq(0,0, X_0, X_1) + v_1\cdot eq(0,1, X_0, X_1) + v_2\cdot eq(1,0, X_0, X_1) + v_3\cdot eq(1,1, X_0, X_1) \]

\[ \tilde{f}_2(X_0, X_1) = v_0'\cdot eq(0,0, X_0, X_1) + v_1'\cdot eq(0,1, X_0, X_1) + v_2'\cdot eq(1,0, X_0, X_1) + v_3'\cdot eq(1,1, X_0, X_1) \]

那么它们的和为：\(\tilde{f}_1(X_0, X_1) + \tilde{f}_2(X_0, X_1)\)，其点值式为：

\[\begin{split} \begin{split} \tilde{f}_1(X_0, X_1) + \tilde{f}_2(X_0, X_1) &= (v_0+v_0')\cdot eq(0,0, X_0, X_1) + (v_1+v_1')\cdot eq(0,1, X_0, X_1) \\ & \ + (v_2+v_2')\cdot eq(1,0, X_0, X_1) + (v_3+v_3')\cdot eq(1,1, X_0, X_1) \\ \end{split} \end{split}\]

于是下面的等式成立：

TODO: 这里要展开推导

\[ [[\tilde{f}_1(X_0, X_1) + \tilde{f}_2(X_0, X_1)]]_2 = [[\tilde{f}_1(X_0, X_1)]]_2 + [[\tilde{f}_2(X_0, X_1)]]_2 \]

同时不难证明，上面的等式对任意的维度相同的 MLE 多项式都成立。另外也不难证明：

\[ [[\alpha\cdot \tilde{f}]]_n = \alpha\cdot [[\tilde{f}]]_n,\quad \forall \alpha \in \mathbb{F}_q \]

因此，我们说 \([[\tilde{f}]]_n\) 这个映射具有多项式加法同态性，并且是一个一一映射（Injective and Surjective）。

低维到高维的映射

我们考虑更一般多项式的情况，假设一个二维的 MLE 多项式 \(\tilde{c}(X_0, X_1)\)，它在二维 Boolean Hypercube 上的取值为 \((v_0, v_1, v_2, v_3)\)，那么它对应的 Univariate 多项式为：

\[\begin{split} \begin{split} [[\tilde{c}]]_2 &= v_0 + v_1X + v_2X^2 + v_3X^3 \\ \end{split} \end{split}\]

而 \(X_2\cdot \tilde{c}(X_0, X_1)\) 也同样是一个 MLE 多项式，维度为 3 。它在三维 Boolean Hypercube 上的取值为： \((0, 0, 0, 0, v_0, v_1, v_2, v_3)\) ，即前四项为零，后四项等于 \(\tilde{c}(X_0, X_1)\) 在二维 Boolean Hypercube 上的取值，如下图所示：

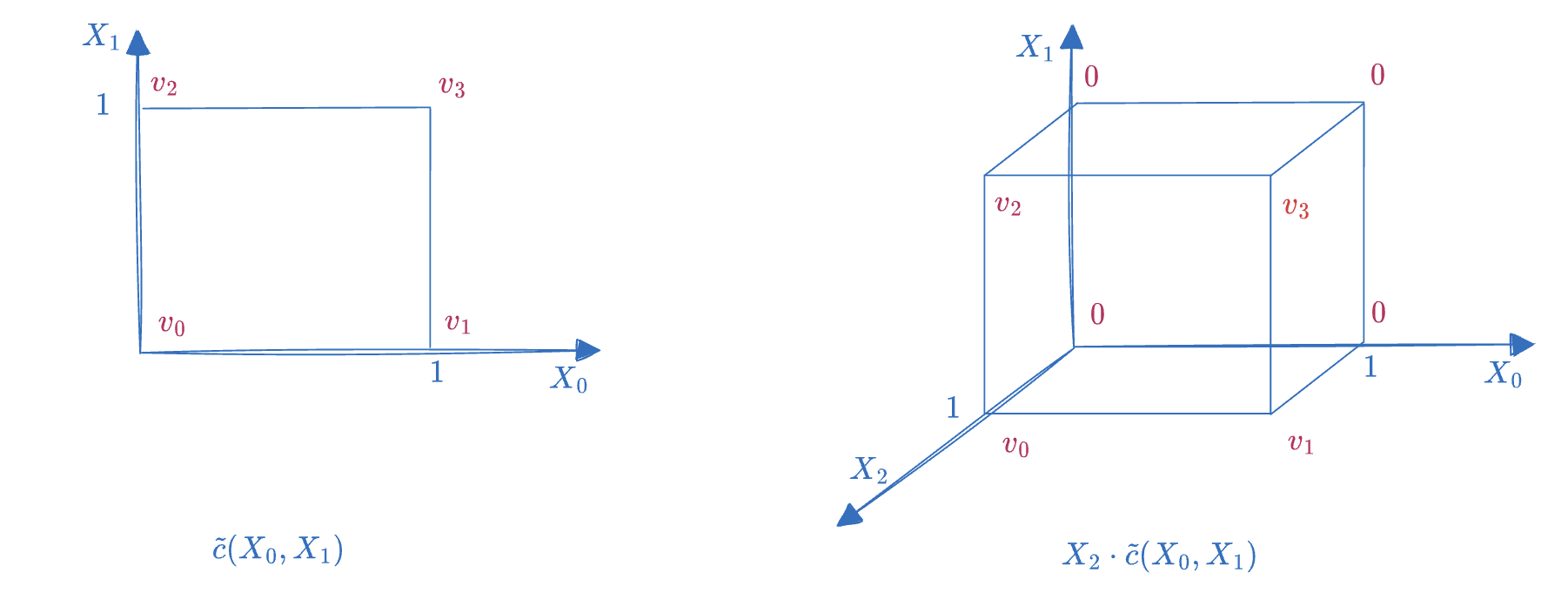
这个容易解释，因为当 \(X_2=0\) 时，整体多项式取值为零，于是 \(X_0, X_1\) 构成的二维正方形顶点上的值都为零，而当 \(X_2=1\) 时，多项式 \(X_2\cdot \tilde{c}(X_0, X_1)\) 等于 \(\tilde{c}(X_0, X_1)\) 。因此 \(X_2=1\) 的平面正方形的顶点上的值等于 \(\tilde{c}(X_0, X_1)\) ，进一步我们可以有这样的结论：

\[ [[X_2\cdot \tilde{c}]]_3 = X^4 \cdot [[\tilde{c}]]_2 \]

快速推导如下 ：

\[ [[X_2\cdot \tilde{c}]]_3 = v_0X^4 + v_1X^5 + v_2X^6 + v_3X^7 = X^4\cdot (v_0 + v_1X + v_2X^2 + v_3X^3) = X^4 \cdot [[\tilde{c}]]_2 \]

这里的 \(X^4\) 推高了 \([[\tilde{c}]]_2\) 的次数，使得它能够刚好放在三维的 Boolean Hypercube 的高位区域（即 \(X_2=1\) 的区域）。

然后考虑下 \(\tilde{c}(X_0, X_1)\) 在三维 Boolean Hypercube 上的取值，我们会发现新增加的未知数 \(X_2\)，不管取值为 0 还是 1，多项式的取值只和 \(X_0, X_1\) 有关，因此，它的点值式等于二维点值向量复制一份，从而填满 3 维的 Hypercube，如下图所示：

换句话说，\(\tilde{c}(X_0, X_1)\) 在三维 Hypercube 上的点值式为 \((v_0, v_1, v_2, v_3, v_0, v_1, v_2, v_3)\)，因此它所映射到的 Univariate 多项式为：

\[\begin{split} \begin{split} [[\tilde{c}]]_3 &= v_0 + v_1X + v_2X^2 + v_3X^3 + v_0X^4 + v_1X^5 + v_2X^6 + v_3X^7 \\ & = (1 + X^4)\cdot (v_0 + v_1X + v_2X^2 + v_3X^3) \\ & = (1 + X^4)\cdot [[\tilde{c}]]_2 \end{split} \end{split}\]

上面的等式可以这么解释：三维 Hypercube 上的取值由两部分拼接而成，\([[\tilde{c}]]_2\) 与由 \(X^4\) 推高次数的 \([[\tilde{c}]]_2\)。

同理可推，\(\tilde{c}(X_0, X_1)\) 在四维 Hypercube 上的取值为 \((v_0, v_1, v_2, v_3, \quad v_0, v_1, v_2, v_3, \quad v_0, v_1, v_2, v_3, \quad v_0, v_1, v_2, v_3)\)，那么它所映射到的 Univariate 多项式为：

\[\begin{split} \begin{split} [[\tilde{c}]]_4 &= v_0 + v_1X + v_2X^2 + v_3X^3 + v_0X^4 + v_1X^5 + v_2X^6 + v_3X^7 + v_0X^8 + v_1X^9 + v_2X^{10} + v_3X^{11} + v_0X^{12} + v_1X^{13} + v_2X^{14} + v_3X^{15} \\ & = (1 + X^4 + X^8 + X^{12})\cdot (v_0 + v_1X + v_2X^2 + v_3X^3) \\ & = (1 + X^4 + X^8 + X^{12})\cdot [[\tilde{c}]]_2 \end{split} \end{split}\]

把低维的 MLE 拉升到一个高维的 Hypercube 上，就会出现低维 Hypercube 不断复制自己的现象。我们可以定义一个新的多项式函数，\(\Phi_k(X)\)，来表示这种周期性的复制操作：

\[ \Phi_k(X^h) = 1 + X^h + X^{2h} + \ldots + X^{(2^{k}-1)h} \]

显然，\([[\tilde{c}]]_4=\Phi_1(X^4)\cdot [[\tilde{c}]]_2\)。

MLE 多项式的除法分解

接下来的问题是：如何利用这个 MLE 到 Unvariate 多项式映射来实现 MLE 的 Evaluation 证明协议。具体点说，如何利用 \(\mathsf{cm}(\tilde{f})\) 来验证 \(\tilde{f}\) 在某个点的取值的正确性，比如 \(\tilde{f}(u_0, u_1)\)？我们虽然已经有了一个基于 KZG10 的 Evaluation Argument 协议，可惜是基于 Univariate 多项式，而非 MLE 多项式。KZG10 利用了 Univariate 多项式的除法分解性质，如下公式

\[ \hat{f}(X) - \hat{f}(z) = q(X)\cdot (X-z) \]

将商多项式 \(q(X)\) 的承诺 \(\mathsf{cm}(q)\) 作为 Evaluation 的证明。那么我们如何将 MLE 在一个多维空间的点，比如 \((u_0, u_1, \ldots, u_{n-1})\) 上的 Evaluation 证明问题，转化为 Univariate 多项式在一个点或多个点上的 Evaluation 证明呢？

论文 [PST13] 给出了一个上述定理的多元多项式版本：

\[ f(X_0, X_1, \ldots, X_{n-1}) - f(u_0, u_1, \ldots, u_{n-1})= \sum_{k=0}^{n-1}q_k(X_0, X_1, \ldots, X_{n-1}) \cdot (X_k - u_k) \]

如果 \(f(X_0, X_1, \ldots, X_{n-1})\) 是一个 MLE 多项式，那么它可以被简化为下面的公式：

\[\begin{split} \begin{split} \tilde{f}(X_0, X_1, \ldots, X_{n-1}) - \tilde{f}(u_0, u_1, \ldots, u_{n-1}) & = \tilde{q}_{n-1}(X_0, X_1, \ldots, X_{\color{red}n-2}) \cdot (X_{n-1} - u_{n-1}) \\ & + \tilde{q}_{n-2}(X_0, X_1, \ldots, X_{\color{red}n-3}) \cdot (X_{n-2} - u_{n-2}) \\ & + \cdots \\ & + \tilde{q}_{1}(X_0) \cdot (X_{1} - u_{1}) \\ & + \tilde{q}_{0} \cdot (X_{0} - u_{0}) \\ \end{split} \end{split}\]

这是因为 MLE 多项式 \(f(X_0, X_1, \ldots, X_{n-1})\) 中每一个未知数的最高次数为 \(1\)，对于 \(f(X_0, X_1, \ldots, X_{k})\)，它除以 \((X_k-u_k)\) 因式之后，余数多项式中将不再含有未知数 \(X_k\) ，所以当 \(f(X_0, X_1, \ldots, X_{n-1})\) 依次除以 \((X_{n-1} - u_{n-1})\) 到 \((X_0 - u_0)\) 这些因式，我们得到的商多项式和余数多项式中的未知数个数一直在逐个减少，直到最后得到一个常数的商多项式 \(\tilde{q}_0\)，当然还有一个常数的余数多项式，而后者正好是 MLE 多项式在 \((u_0, u_1, \ldots, u_{n-1})\) 处的求值。

我们假设这个最后的求值为 \(v\) ，即

\[ \tilde{f}(u_0, u_1, \ldots, u_{n-1}) = v \]

那么我们对余数定理等式的左右两边（都看成是一个 MLE 多项式）分别进行 Zeromorph 映射，得到对应的 Univariate 多项式。

\[ [[\tilde{f}(X_0, X_1, \ldots, X_{n-1}) - v]]_n= [[\sum_{k=0}^{n-1}\tilde{q}_k(X_0, X_1, \ldots, X_{\color{red}k-1}) \cdot (X_k - u_k)]]_n \]

由于映射具有加法的同态性，因此我们可以继续化简上面的等式：

\[\begin{split} \begin{split} [[\tilde{f}(X_0, X_1, \ldots, X_{n-1})]]_n - [[v]]_n &= \sum_{k=0}^{n-1}[[\tilde{q}_k(X_0, X_1, \ldots, X_{k-1}) \cdot (X_k - u_k)]]_n \\ &= \sum_{k=0}^{n-1}\Big([[X_k\cdot \tilde{q}_k(X_0, X_1, \ldots, X_{k-1})]]_n - u_k[[\tilde{q}_k(X_0, X_1, \ldots, X_{k-1})]]_n\Big) \end{split} \end{split}\]

先看等式左边的 \([[\tilde{f}(X_0,X_1,\ldots, X_{n-1})]]_n\) 这一项直接映射到 \(\hat{f}(X)\)，再看 \([[v]]_n\) 这一项，它映射到 \(\hat{v}(X)\)，

\[ [[v]]_n = \hat{v}(X) = v + vX + vX^2 + \ldots + vX^{2^n-1} \]

或者我们改用 \(\Phi_n(X)\) 函数来表示：

\[ [[v]]_n = v\cdot\Phi_n(X) \]

看下等式右边的 \([[\tilde{q}_k(X_0, X_1, \ldots, X_{k-1})]]_n\)，这一项是将 \(k\) 维的 Hypercube填充到 \(n\) 维的 Hypercube 上，然后再进行映射。根据前面的讨论，我们需要将 \(k\) 维的 Hypercube 连续复制 \(2^{n-k}\) 次，从而填满 \(n\) 维 Hypercube：

\[ [[\tilde{q}_k(X_0, X_1, \ldots, X_{k-1})]]_n = \Phi_{n-k}(X^{2^k})\cdot [[\tilde{q}_k(X_0, X_1, \ldots, X_{k-1})]]_{k} \]

再解释下, \(\Phi_{n-k}(X^{2^k})\) 定义展开如下：

\[ \Phi_{n-k}(X^{2^k}) = 1 + X^{2^k} + X^{2\cdot 2^k} + \ldots + X^{(2^{n-k}-1)\cdot 2^k} \]

它的系数为一个若干个 \(0,1\) 组成，并且每两个 \(1\) 之间位置间隔为 \(2^k\)：

\[ (1, 0, 0 ,\ldots, 0, \quad 1, 0 ,\ldots, 0, \quad 1, 0 ,\ldots, 0, \quad 1) \]

假设有一个次数受限的多项式 \(g(X)\in\mathbb{F}_q[X]\)，满足 \(\deg(g)<2^k\) ，那么多项式 \(\Phi_{n-k}(X^{2^k})\cdot g\) 就表示了一个 \(2^k-1\) 次多项式 \(g(X)\) 被 \(2^k\) 间隔的系数向量重复了 \(2^{n-k}\) 次，最终得到了一个 \(2^n-1\) 次的多项式。

最后还剩下 \([[X_k\cdot \tilde{q}_k(X_0, X_1, \ldots, X_{k-1})]]_n\) 这项，如何继续化简它呢？

我们可以分两步来构造它的映射，首先看 \(\tilde{q}_k(X_0, X_1, \ldots, X_{k-1})\) 可以由一个 k 维 Boolean Hypercube 表示，然后当乘以一个新的未知数 \(X_k\)，它就变成了一个需要 \(k+1\) 维的 Boolean Hypercube 表示的 MLE 多项式。而这个新 Boolean Hypercube 可以分为两部分，一部分都是零（当 \(X_k=0\) 时），另一部分正是 \(\tilde{q}_k(X_0, X_1, \ldots, X_{k-1})\) （当 \(X_k=1\) 时）。所以我们先利用 \(\Phi_n(X)\) 函数，构造一个 Boolean Hypercube 的重复模式，其中间隔为 \(2^{k+1}\)，然后把 \(k\) 维 Boolean Hypercube 进行 \(2^{n-k-1}\) 次复制，于是我们得到了下面的多项式。

\[ \Phi_{n-k-1}(X^{2^{k+1}})\cdot [[\tilde{q}_k(X_0, X_1, \ldots, X_{k-1})]]_{k} \]

不过这只是第一步。上面这个 Univariate 多项式和 \([[X_k\cdot \tilde{q}_k(X_0, X_1, \ldots, X_{k-1})]]_n\) 还不相等，因为前者在每一个重复的 \(k+1\) 维 Boolean Hypercube 中，\(X_k=1\) 部分为零，而 \(X_k=0\) 部分放的则是 \(k\) 维 Boolean Hybercube \(\tilde{q}_k(X_0, X_1, \ldots, X_{k-1})\)，这与我们想要的 Boolean Hypercube 不同。我们需要再为它补上 \(X^{2^k}\) 这样的移位因子，这样就可以调换 \(X_k\) 所对应的 \(k\) 维的 Boolean Hypercube 的位置（从低位区域转移到高位区域）。映射后的结果为：

\[ [[X_k\cdot \tilde{q}_k(X_0, X_1, \ldots, X_{k-1})]]_n = X^{2^k}\cdot \Phi_{n-k-1}(X^{2^{k+1}})\cdot [[\tilde{q}_k(X_0, X_1, \ldots, X_{k-1})]]_{k} \]

下图用一个特定的例子演示，其中 \(k=3, n=5\)， 左边为移位前的 \(5\) 维 Boolean Hypercube，其中上下两半场表示第五个维度，每个半场有两个三维立方体，表示第四个维度。我们可以看到，仅当 \(X_3=0\) 的三维立方体恰好对应 \(\tilde{f}(X_0, X_1, X_2)\)，而当 \(X_3=1\) 时，三维立方体上全为零。而下图右边为移位后的 \(5\) 维 Boolean Hypercube，其中的 \(\tilde{f}(X_0, X_1, X_2)\) 立方体被移位到了右边，也就是 \(X_3=1\) 所对应的区域。

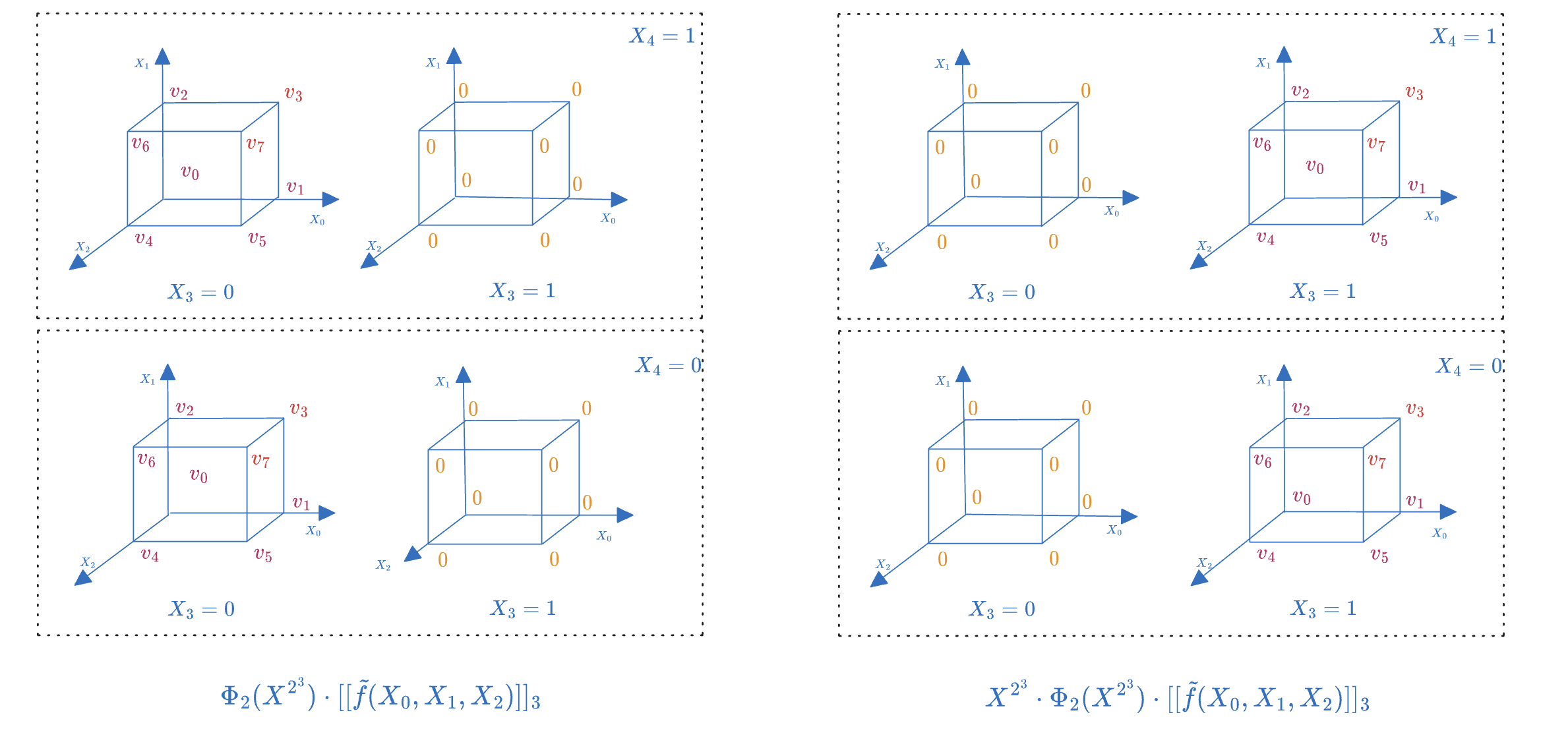
到此，我们可以得到 Zeromorph 协议的关键等式：

\[ \begin{split} [[\tilde{f}(X_0, X_1, \ldots, X_{n-1})]]_n - v\cdot\Phi_n(X) &=\sum_{k=0}^{n-1}\Big(X^{2^k}\cdot \Phi_{n-k-1}(X^{2^{k+1}}) - u_k\cdot\Phi_{n-k}(X^{2^k})\Big)\cdot [[\tilde{q}_k(X_0, X_1, \ldots, X_{k-1})]]_k \end{split} \]

基于 KZG10 的 Evaluation Argument

注意到上节我们推导出的 Zeromorph 等式是一个关于 Univariate 多项式的等式，我们简写为：

\[ \hat{f}(X) - v\cdot\Phi_n(X) = \sum_k \Big(X^{2^k}\cdot \Phi_{n-k-1}(X^{2^{k+1}}) - u_k\cdot\Phi_{n-k}(X^{2^k})\Big)\cdot \hat{q}_k(X) \]

这里 \(\hat{f}(X)\) 与 \(\hat{q}_k(X)\) 定义如下：

\[\begin{split} \begin{split} \hat{f}(X) &= [[\tilde{f}(X_0, X_1, \ldots, X_{n-1})]]_n \\ \hat{q}_k(X) &= [[\tilde{q}_k(X_0, X_1, \ldots, X_{k-1})]]_k\\ \end{split} \end{split}\]

我们要证明 \(\tilde{f}(X_0, X_1, \ldots, X_{n-1})\) 在点 \((u_0, u_1, \ldots, u_{n-1})\) 处的取值为 \(v\)，那么我们只需要检查上面的多项式是否相等即可。这里利用 Schwartz-Zippel 引理的思想，让 Verifier 随机挑选一个点 \(X=\zeta\) ，然后让 Prover 提供 \(\hat{f}(\zeta)\) 和 \(\hat{q}_k(\zeta)\) 的值，以便于 Verifier 验证下面的等式是否成立：

\[ \hat{f}(\zeta) - v\cdot\Phi_n(\zeta) = \sum_k \Big(\zeta^{2^k}\cdot \Phi_{n-k-1}(\zeta^{2^{k+1}}) - u_k\cdot\Phi_{n-k}(\zeta^{2^k})\Big)\cdot \hat{q}_k(\zeta) \]

不过这还不够，因为 Prover 实际上承诺的是 \(\hat{q}_k(X)\)，为了保证 MLE 余数多项式关系成立，我们要强制要求所有的商多项式 \(\hat{q}_k(X)\) 的次数都小于 \(2^k\)，即 \(\deg(\hat{q}_k)<2^k\)，以确保 Prover 没有作弊的空间。

不管是 FRI 还是 KZG10，都提供了证明 \(\deg(\hat{q}_k)<2^k\) 的方法。本文我们仅考虑基于 KZG10 的 Zeromorph 协议。一个简单的基于 KZG10 的 Degree Bound 证明协议如下：

• Prover 提供 \(\mathsf{cm}(\hat{q}_k)\) 并附加上 \(\mathsf{cm}(X^{D-2^k+1}\cdot \hat{q}_k(X))\) 发送给 Verifier，

• Verifier 验证下面的等式：

\[ e\big(\mathsf{cm}(\hat{q}_k),\ [\tau^{D-2^k+1}]_2\big) = e\big(\mathsf{cm}(X^{D-2^k+1}\cdot \hat{q}_k(X)),\ [1]_2\big) \]

这里 \(X^{D-2^k+1}\cdot \hat{q}_k(X)\) 的作用是把 \(\hat{q}_k(X)\) 的 Degree 对齐到 \(D\)。因为 KZG10 的 SRS 中，能承诺的多项式的 Degree 最多为 \(D\)，所以如果 \(\hat{q}_k(X)\) 的 Degree 超过了 \(2^k\)，那么 \(\deg(X^{D-2^k+1}\cdot \hat{q}) > D\)，这样就无法用 KZG10 的 SRS 中进行承诺。反之如果 Prover 可以正确承诺 \(X^{D-2^k+1}\cdot \hat{q}_k(X)\) ，那就证明了 \(\deg(\hat{q}_k)<2^k\) 。

Evaluation 证明协议

下面我们先给出一个简单朴素的协议实现，方便理解。

公共输入

• MLE 多项式 \(\tilde{f}\) 的承诺 \(\mathsf{cm}([[\tilde{f}]]_n)\)

• 求值点 \(\mathbf{u}=(u_0, u_1, \ldots, u_{n-1})\)

• 求值结果 \(v = \tilde{f}(\mathbf{u})\)

Witness

• MLE 多项式 \(\tilde{f}\) 在 \(n\) 维 Hypercube 上的点值向量 \(\mathbf{a} = (a_0, a_1, \ldots, a_{2^n-1})\)

Round 1

Prover 发送余数多项式的承诺

• 计算 \(n\) 个余数 MLE 多项式， \(\{\tilde{q}_k\}_{k=0}^{n-1}\)

• 构造余数 MLE 多项式所映射到的 Univariate 多项式 \(\hat{q}_k=[[\tilde{q}_k]]_k, \quad 0 \leq k < n\)

• 计算并发送它们的承诺：\(\mathsf{cm}(\hat{q}_0), \mathsf{cm}(\hat{q}_1), \ldots, \mathsf{cm}(\hat{q}_{n-1})\)

\[ \tilde{f}(X_0,X_1,\ldots, X_{n-1}) - v = \sum_{k=0}^{n-1} (X_k-u_k) \cdot \tilde{q}_k(X_0,X_1,\ldots, X_{k-1}) \]

Prover 计算，\(\pi_k=\mathsf{cm}(X^{D_{max}-2^k+1}\cdot \hat{q}_k), \quad 0\leq k<n\) ，作为 \(\deg(\hat{q}_k)<2^k\) 的 Degree Bound 证明 ，一并发送给 Verifier

Round 2

1. Verifier 发送随机数 \(\zeta\in \mathbb{F}_p^*\)

2. Prover 计算辅助多项式 \(r(X)\) 与商多项式 \(h(X)\)，并发送 \(\mathsf{cm}(h)\)

• 计算 \(r(X)\) ，

\[ r(X) = [[\tilde{f}]]_{n} - v\cdot \Phi_{n}(\zeta) - \sum_{k=0}^{n-1} \Big(\zeta^{2^k}\cdot \Phi_{n-k-1}(\zeta^{2^{k+1}}) - u_k\cdot \Phi_{n-k}(\zeta^{2^{k}})\Big)\cdot \hat{q}_k(X) \]

• 计算 \(h(X)\) 及其承诺 \(\mathsf{cm}(h)\)， 作为 \(r(X)\) 在 \(X=\zeta\) 点取值为零的证明

\[ h(X) = \frac{r(X)}{X-\zeta} \]

Verification

Verifier 验证下面的等式

• 构造 \(\mathsf{cm}(r)\) 的承诺：

\[ \mathsf{cm}(r) = \mathsf{cm}([[\tilde{f}]]_{n}) - \mathsf{cm}(v\cdot \Phi_{n}(\zeta)) - \sum_{i=0}^{n-1} \Big(\zeta^{2^i}\cdot \Phi_{n-i-1}(\zeta^{2^{i+1}}) - u_i\cdot \Phi_{n-i}(\zeta^{2^{i}})\Big)\cdot \mathsf{cm}(\hat{q}_i) \]

• 验证 \(r(\zeta) = 0\)

\[ e(\mathsf{cm}(r), \ [1]_2) = e(\mathsf{cm}(h), [\tau]_2 - \zeta\cdot [1]_2) \]

• 验证 \((\pi_0, \pi_1, \ldots, \pi_{n-1})\) 是否正确，即验证所有的余数多项式的 Degree Bound： \(\deg(\hat{q}_i)<2^i\) ，对于 \(0\leq i<n\)

\[ e(\mathsf{cm}(\hat{q}_i), [\tau^{D_{max}-2^i+1}]_2) = e(\pi_i, [1]_2), \quad 0\leq i<n \]

效率概述

• 证明尺寸： \((2n+1)\mathbb{G}_1\)

• Verifier 计算量： \((2n +2) P\)，\((n+2)\mathsf{EccMul}^{\mathbb{G}_1}\)

优化协议

朴素协议中有 \(n\) 个商多项式，它们的 Degree Bound 有 \(2n\) 个 \(\mathbb{G}_1\) ，这显然不够高效。不过，我们可以批量地证明这 \(n\) 个 degree bound。下面是传统的批量证明的思路：

• Verifer 先发送一个随机数 \(\beta\)

• Prover 把 \(n\) 个商多项式聚合在一起，得到 \(\bar{q}(X)\)，聚合的时候把这些商多项式的 Degree 补齐到同一个值，即 \(2^n - 1\) ：

\[ \bar{q}(X) = \sum_{k=0}^{n-1} \beta^k \cdot X^{2^n-2^k}\cdot \hat{q}_k(X) \]

• Prover 发送 \(\bar{q}(X)\) 的承诺 \(\mathsf{cm}(\bar{q})\)

• Verifier 发送随机数 \(\zeta\)

• Prover 构造多项式 \(s(X)\)，它在 \(X=\zeta\) 处取值为零，即 \(s(\zeta)=0\)

\[ s(X) = \bar{q}(X) - \sum_{k=0}^{n-1} \beta^k \cdot \zeta^{2^n-2^k}\cdot \hat{q}_k(X) \]

• Prover 构造商多项式 \(h_1(X)\) 并将其 Degree 对齐到最大的 Degree Bound \(D\)，然后证明 \(s(\zeta)=0\) ，并发送承诺 \(\mathsf{cm}(h_1)\)

\[ h_1(X) = \frac{s(X)}{X-\zeta}\cdot X^{D-2^n+2} \]

• Verifier 手里有 \(\mathsf{cm}(\bar{q})\) 与 \(\mathsf{cm}(\hat{q}_i)\)，他可以根据下面的等式，还原出 \(\mathsf{cm}(s)\) 的承诺：

\[ \mathsf{cm}(s) = \mathsf{cm}(\bar{q}) - \sum_{i=0}^{n-1} \beta^i \cdot \zeta^{2^n-2^k}\cdot \mathsf{cm}(\hat{q}_i) \]

• Verifier 只需要两个 Pairing 运算即可验证 \(s(\zeta)=0\)，从而得到 \(n\) 个 Degree Bound 证明成立

\[ e\big(\mathsf{cm}(s), \ [\tau^{D_{max}-2^n+2}]_2\big) = e\big(\mathsf{cm}(h_1), [\tau]_2 - \zeta\cdot [1]_2\big) \]

此外，Verfier 还可以发一个随机数 \(\alpha\)，进一步聚合 \(r(X)\) 与 \(s(X)\) 的取值证明，因为它们两个在 \(X=\zeta\) 处的取值都为零。

下面是优化版本的 Zeromorph 协议，参见 Zeromorph 论文 [KT23] Section 6。优化的技术主要是将多个 Degree Bound 证明聚合在一起，同时将 \(r(X)\) 的求值证明也聚合在一起。这样可以仅使用两个 Pairing 运算来验证验证（这个版本暂时不考虑 Zero-knowledge 的性质）。

Evaluation 证明协议

公共输入

• MLE 多项式 \(\tilde{f}\) 映射到 Univariate 多项式 \(f(X)=[[\tilde{f}]]_n\) 的承诺 \(\mathsf{cm}([[\tilde{f}]]_n)\)

• 求值点 \(\mathbf{u}=(u_0, u_1, \ldots, u_{n-1})\)

• 求值结果 \(v = \tilde{f}(\mathbf{u})\)

Witness

• MLE 多项式 \(\tilde{f}\) 的求值向量 \(\mathbf{a} = (a_0, a_1, \ldots, a_{2^n-1})\)

Round 1

第一轮：Prover 发送余数多项式的承诺

• 计算 \(n\) 个余数 MLE 多项式， \(\{q_i\}_{i=0}^{n-1}\)

• 构造余数 MLE 多项式所映射到的 Univariate 多项式 \(\hat{q}_i=[[q_i]]_i, \quad 0 \leq i < n\)

• 计算并发送它们的承诺：\(\mathsf{cm}(\hat{q}_0), \mathsf{cm}(\hat{q}_1), \ldots, \mathsf{cm}(\hat{q}_{n-1})\)

\[ \tilde{f}(X_0,X_1,\ldots, X_{n-1}) - v = \sum_{i=0}^{n-1} (X_k-u_k) \cdot q_i(X_0,X_1,\ldots, X_{k-1}) \]

Round 2

1. Verifier 发送随机数 \(\beta\in \mathbb{F}_p^*\) 用来聚合多个 Degree Bound 证明

2. Prover 构造 \(\bar{q}(X)\) 作为聚合商多项式 \(\{\hat{q}_i(X)\}\) 的多项式，并发送其承诺 \(\mathsf{cm}(\bar{q})\)

\[ \bar{q}(X) = \sum_{i=0}^{n-1} \beta^i \cdot X^{2^n-2^i}\hat{q}_i(X) \]

Round 3

1. Verifier 发送随机数 \(\zeta\in \mathbb{F}_p^*\) ，用来挑战多项式在 \(X=\zeta\) 处的取值

2. Prover 计算 \(h_0(X)\) 与 \(h_1(X)\)

• 计算 \(r(X)\) ，

\[ r(X) = \hat{f}(X) - v\cdot \Phi_{n}(\zeta) - \sum_{i=0}^{n-1} \Big(\zeta^{2^i}\cdot \Phi_{n-i-1}(\zeta^{2^{i+1}}) - u_i\cdot \Phi_{n-i}(\zeta^{2^{i}})\Big)\cdot\hat{q}_i(X) \]

• 计算 \(s(X)\) ，

\[ s(X) = \bar{q}(X) - \sum_{k=0}^{n-1} \beta^k \cdot \zeta^{2^n-2^k}\cdot \hat{q}_k(X) \]

• 计算商多项式 \(h_0(X)\) 与 \(h_1(X)\)

\[ h_0(X) = \frac{r(X)}{X-\zeta}, \qquad h_1(X) = \frac{s(X)}{X-\zeta} \]

Round 4

1. Verifier 发送随机数 \(\alpha\in \mathbb{F}_p^*\) ，用来聚合 \(h_0(X)\) 与 \(h_1(X)\)

2. Prover 计算 \(h(X)\) 并发送其承诺 \(\mathsf{cm}(h)\)

\[ h(X)=(h_0(X) + \alpha\cdot h_1(X))\cdot X^{D_{max}-2^n+2} \]

Verification

Verifier

• 构造 \(\mathsf{cm}(r)\) 的承诺：

\[ \mathsf{cm}(r) = \mathsf{cm}(f) - \mathsf{cm}(v\cdot \Phi_{n}(\zeta)) - \sum_{i=0}^{n-1} \Big(\zeta^{2^i}\cdot \Phi_{n-i-1}(\zeta^{2^{i+1}}) - u_i\cdot \Phi_{n-i}(\zeta^{2^{i}})\Big)\cdot \mathsf{cm}(\hat{q}_i) \]

• 构造 \(\mathsf{cm}(s)\) 的承诺：

\[ \mathsf{cm}(s) = \mathsf{cm}(\bar{q}) - \sum_{i=0}^{n-1} \beta^i \cdot \zeta^{2^n-2^i}\cdot \mathsf{cm}(\hat{q}_i) \]

• 验证 \(r(\zeta) = 0\) 与 \(s(\zeta) = 0\)

\[ e(\mathsf{cm}(r) + \alpha\cdot \mathsf{cm}(s), \ [\tau^{D-2^n+2}]_2) = e(\mathsf{cm}(h),\ [\tau]_2 - \zeta\cdot [1]_2) \]

总结

Zeromorph 总体上来说是一个简洁的协议，它将 MLE 的点值式直接映射到 Univariate 多项式的系数，然后利用 KZG10 协议来完成 Evaluation 的证明。后续文章将讨论如何将 Zeromorph 结合 FRI 协议来实现 MLE PCS。

Reference:

• [KT23] Kohrita, Tohru, and Patrick Towa. “Zeromorph: Zero-knowledge multilinear-evaluation proofs from homomorphic univariate commitments.” Cryptology ePrint Archive (2023). https://eprint.iacr.org/2023/917

• [PST13] Papamanthou, Charalampos, Elaine Shi, and Roberto Tamassia. “Signatures of correct computation.” Theory of Cryptography Conference. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013. https://eprint.iacr.org/2011/587