STIR: 提升码率来降低查询复杂度

STIR: 提升码率来降低查询复杂度#

本文主要受 STIR 论文 作者的博客文章 STIR: Reed–Solomon Proximity Testing with Fewer Queries 与演讲 ZK11: STIR: Reed–Solomon Proximity Testing with Fewer Queries - Gal Arnon & Giacomo Fenzi 的启发，介绍 STIR 协议。

STIR 和 FRI 一样，也是解决 Reed-Solomon Proximity Testing 问题，不过与 FRI 相比，其有更低的查询复杂度，这会降低 argument 的大小与 Verifier 的哈希复杂度。那么 STIR 是如何实现这一点的呢？其实谜底就在谜面上，STIR 取了 Shift To Improve Rate 的首字母，STIR 的核心点就在其通过每次移动 evaluation domain，来提升码率。直观地理解，码率实际刻画的是码字中所含的真实信息的比例，码率降低，真实信息减少，对应码字中的冗余就增大了，Verifier 就更容易测试接受到的一个消息到该编码空间的 proximity 了，其测试能力变得更强了。换句话说，由于 Verifier 的测试能力变强，那么其只需要更少的查询次数就能达到目标的安全性了。下面通过对比 FRI 和 STIR，来看看 STIR 是如何降低码率的。

FRI v.s. STIR#

对于一个有限域 \(\mathbb{F}\) ，取 \(\mathcal{L} \subseteq \mathbb{F}\) 为 evaluation domain，设其大小 \(|\mathcal{L}| = n\)，用 \(d\) 表示次数界限(不妨设 \(n\) 与 \(d\) 都是 \(2\) 的幂次)，那么 Reed-Solomon 编码空间 \(\mathrm{RS}[\mathbb{F},\mathcal{L},d]\) 包含的是所有这样的函数 \(f: \mathcal{L} \rightarrow \mathbb{F}\) ，函数 \(f\) 能与一个次数严格小于 \(d\) 的多项式在 \(\mathcal{L}\) 上的求值完全一致。码率 \(\rho := d/|\mathcal{L}|\) 。

协议的目标是解决 Reed-Solomon Proximity Testing 问题，其中 Verifier 是可以通过查询获得一个函数 \(f: \mathcal{L} \rightarrow \mathbb{F}\) 的，那么 Verifier 的目标就是在尽可能少的位置上查询 \(f\) 的值，能够区分出 \(f\) 属于下面哪一种情况：

  1. \(f\) 是一个 Reed-Solomon 码字，即 \(f \in \mathrm{RS}[\mathbb{F},\mathcal{L},d]\) ；

  2. \(f\) 距离 Reed-Solomon 编码空间 \(\mathrm{RS}[\mathbb{F},\mathcal{L},d]\) 中的所有码字的相对 Hamming 距离都有 \(\delta\) 那么远，即 \(\Delta(f, \mathrm{RS}[\mathbb{F},\mathcal{L},d]) > \delta\) 。

我们在 IOPP(Interactive Oracle Proofs of Proximity) 模型下考虑上述 Reed-Solomon Proximity Testing 问题，此时 Verifier 可以和 Prover 进行交互，并且能通过 oracle 获得 Prover 的消息，如下图所示。

Verifier 通过与 Prover 一系列交互之后，分两种情况：

  • \(f \in \mathrm{RS}[\mathbb{F},\mathcal{L},d]\) ，Verifier 接受 :)

  • \(\Delta(f, \mathrm{RS}[\mathbb{F},\mathcal{L},d]) > \delta\) ，Verifier 大概率拒绝 :(

我们在 \(k\) 折的情况下对比 FRI 协议和 STIR 协议，如下图所示。

在 FRI 协议中，假设 \(g_1\) 是通过随机数 \(\alpha_1\) 进行 \(k\) 折得到的，其中 \(\mathcal{L}^{k} = \{x^k,x\in \mathcal{L}\}\) 。因此将测试 \(f \in \mathrm{RS}[\mathbb{F},\mathcal{L},d]\) 转换为 \(g_1 \in \mathrm{RS}[\mathbb{F},\mathcal{L}^k,d/k]\) ，递归地来测试 \(g_i \in \mathrm{RS}[\mathbb{F},\mathcal{L}^{k^i},d/k^i]\) 。因此在第 \(i\) 轮，其码率

\[ \rho_i = \frac{\frac{d}{k^i}}{|\mathcal{L}_i|} = \frac{d}{k^i} \cdot \frac{k^i}{n} = \frac{d}{n} = \rho \]

可以发现在每一轮中，码率 \(\rho_i\) 始终为 \(\rho\) ，保持不变。

而在 STIR 协议中，注意 \(g_1'\) 仍然是 \(k\) 折，但是其 evaluation domain \(\mathcal{L}'\) 的大小却不是缩小 \(k\) 倍，而是 \(2\) 倍。此时将测试 \(f \in \mathrm{RS}[\mathbb{F},\mathcal{L},d]\) 转换为测试 \(g_1' \in \mathrm{RS}[\mathbb{F},\mathcal{L}',d/k]\) 。那么在第 \(i\) 轮，需要测试 \(g_i' \in \mathrm{RS}[\mathbb{F},\mathcal{L}_{i}',d/k^i]\) 。这时

\[ \rho_i = \frac{\frac{d}{k^i}}{|\mathcal{L}'_i|} = \frac{d}{k^i} \cdot \frac{2^i}{n} = \left( \frac{2}{k}\right)^i \cdot \frac{d}{n} = \left( \frac{2}{k}\right)^i \cdot \rho \]

如果 \(\frac{2}{k} < 1\) 即 \(k > 2\) ，可以发现码率 \(\rho_{i}\) 每一轮都在减小，这就是 STIR 降低查询复杂的关键之处。

当我们将上述的 IOPP 编译成 SNARK 时，需要用到 BCS 转换 ([BCS16], BCS transformation) ，分为两步：

  1. 将 Prover 的消息进行 Merkle 承诺，当 Verifier 想要查询时就打开这些承诺，这一步将 IOPP 转换为了一个简洁的交互论证(succinct interactive argument) 。

  2. 使用 Fait-Shamir 转换将第一步得到的简洁的交互论证转换为非交互的。

在BCS转换中，就需要 IOPP 有一个比较强的 soundness 性质，称为 round-by-round soundness，意思是要求 IOPP 在每一轮有比较小的 soundness error，这比要求整个 IOPP 有比较小的 soundness error 要求更强。我们假设要求 round-by-round soundness error 的界为 \(2^{-\lambda}\) 。每一轮可以重复查询 \(t_{i}\) 次，整个 IOPP 协议进行 \(M\) 轮，那么整个证明的总查询复杂度就为 \(\sum_{i = 0}^M t_i\) 。对于 \(\delta\) 达到 Johnson bound，即 \(\delta = 1 - \sqrt{\rho}\) ，通过计算可以得到

  1. FRI 的查询复杂度为：

    \[ O \left( \lambda \cdot \frac{\log d}{- \log \sqrt{\rho}} \right) \]

  2. STIR 的查询复杂度为：

    \[ O \left( \lambda \cdot \log \left( \frac{\log d}{- \log \sqrt{\rho}} \right) + \log d \right) \]

在 STIR 查询复杂度中，\(d\) 通常不大，因此占比比较大的是第一项 \(\lambda \cdot \log \left( \frac{\log d}{- \log \sqrt{\rho}} \right)\) ，可以发现其是 \(\log \log\) 级别的，而原来的 FRI 只是 \(\log\) 级别。

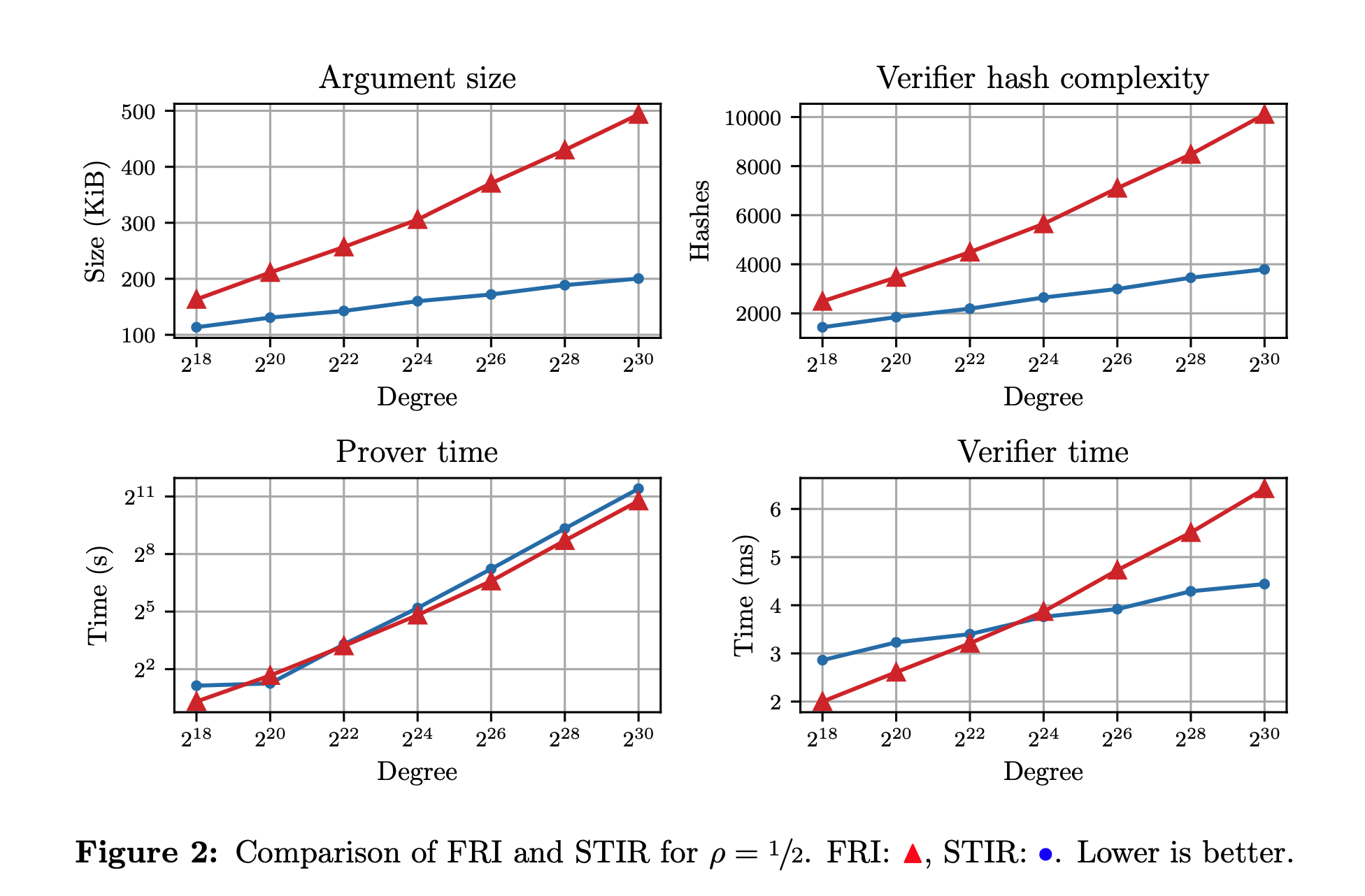
在论文 [ACFY24] 6.4 节中的图 2 给出了 FRI 和 STIR 的对比试验结果，可以发现 STIR 降低查询复杂度导致了其在 argument 大小和 Verifier 计算的哈希数量相比 FRI 更优。这也比较好理解，更少的查询复杂度意味着：

  1. 减少整个 argument 大小是显然的。

  2. 由于查询次数更少，那么 Verifier 需要打开的 Merkle 承诺就更少，计算对应的哈希数量就更少。

关于 RS 编码的强有力的工具#

在这里先引入几个关于 RS 编码的强大工具，其能帮助我们理解具体的 STIR 协议构造。

Folding#

对于一个函数 \(f: \mathcal{L} \rightarrow \mathbb{F}\) ，给一个随机数 \(r \in \mathbb{F}\) ，其 \(k\) 次折叠之后的函数记为 \(f_r := \mathrm{Fold}(f,r) : \mathcal{L}^{k} \rightarrow \mathbb{F}\) 。其定义为，对于每一个 \(x \in \mathcal{L}^{k}\) ，在 \(\mathcal{L}\) 中能找到 \(k\) 个 \(y\) 满足 \(y^k = x\) ，由 \(k\) 对 \((y, f(y))\) 可以得到唯一的一个次数小于 \(k\) 的多项式 \(\hat{p}\) ，其满足 \(\hat{p}(y) = f(y)\) ，那么 \(\hat{p}(r)\) 就是函数 \(f_r(x)\) 的值。这个 Fold 函数的定义和 FRI 协议中的 Fold 函数定义完全一致，其有两个很好的性质。

第一个性质是距离的保持。

  1. 如果折叠前的函数 \(f \in \mathrm{RS}[\mathbb{F}, \mathcal{L}, d]\) ，那么对于任意选取的随机数 \(r \in \mathbb{F}\) ，都有折叠之后的函数依然是 RS 码，即 \(f_r \in \mathrm{RS}[\mathbb{F}, \mathcal{L}^k, d/k]\) 。

  2. 对于 \(\delta \in (0, 1 - \sqrt{\rho})\) ，如果 \(f\) 距离 \(\mathrm{RS}[\mathbb{F}, \mathcal{L}, d]\) 有 \(\delta\) 远，那么以至少 \(1 - \mathrm{poly}(|\mathcal{L}|)/\mathbb{F}\) 的概率对随机数 \(r\) 进行选择，有 \(f_r\) 距离 \(\mathrm{RS}[\mathbb{F}, \mathcal{L}^k, d/k]\) 有 \(\delta\) 远。

这个性质保证了我们可以大胆进行折叠，如果 Prover 作弊，提供了距离编码空间有 \(\delta\) 远的函数，极大概率其折叠之后的函数依然距离对应的编码空间有 \(\delta\) 远。

第二个性质称为 Local，意思是如果要得到折叠后的函数在任意一点的值，只需要查询 \(f\) 在 \(k\) 个点的值就能计算得出，因为此时可以得到唯一一个次数小于 \(k\) 的多项式 \(\hat{p}\) ，再带入 \(r\) 计算得到 \(\hat{p}(r)\) 就是该点的值。此时 Prover 也不需要单独提供 \(\mathrm{Fold}(f,r)\) 的 oracle 了，Verifier 通过访问 \(f\) 的 oracle 就能得到了，这就减少了 argument 大小。

Quotienting#

对于函数 \(f: \mathcal{L} \rightarrow \mathbb{F}\) ，以及 \(p: S \rightarrow \mathbb{F}\) ，其中 \(S \subseteq \mathbb{F}\) ，则关于函数 \(f\) 的 quotient 定义为：

\[ \mathrm{Quotient}(f, S, p)(x) := \frac{f(x) - \hat{p}(x)}{\prod_{a \in S}(X - a)}, \]

其中 \(\hat{p}\) 是满足对任意的 \(a \in S\) ，都有 \(\hat{p}(a) = p(a)\) 的次数小于 \(|S|\) 的唯一的多项式。

该函数的一个重要性质是一致性(Consistency) ，假设 \(S\) 与 \(\mathcal{L}\) 不相交(其实也可以相交，结论会更复杂些，见[ACFY24] Lemma 4.4)，那么

  1. 如果 \(f \in \mathrm{RS}[\mathbb{F}, \mathcal{L}, d]\) ，其是一个次数小于 \(d\) 的多项式在 \(\mathcal{L}\) 上的 evaluation，并且该多项式在 \(S\) 上与 \(p\) 一致，那么 \(\mathrm{Quotient}(f, S, p) \in \mathrm{RS}[\mathbb{F}, \mathcal{L}, d - |S|]\) 。

  2. 如果对于任意一个离 \(f\) 有 \(\delta\) 近的次数小于 \(d\) 的多项式 \(\hat{u}\) ，都有 \(\hat{u}\) 与 \(p\) 在 \(S\) 上不完全一致，即对于一些 \(a \in S\) ，有 \(\hat{u}(a) \neq p(a)\) ，那么 \(\mathrm{Quotient}(f, S, p)\) 距离 \(\mathrm{RS}[\mathbb{F}, \mathcal{L}, d - |S|]\) 就有 \(\delta\) 远。

对于上述第 2 点，在 \(f\) 的 \(\delta\) 范围内的码字 \(\hat{u}\) ，这些码字组成的集合记为 \(\mathrm{List}(f,d,\delta)\) 。对于任意的 \(\hat{u} \in \mathrm{List}(f,d,\delta)\) ，只要在 \(S\) 上有一点，使得 \(\hat{u}(a) \neq p(a)\) ，商多项式 \(\mathrm{Quotient}(f, S, p)\) 的距离就被放大了，就有 \(\delta\) 那么远了，也就是如果这里被除了错误的值 \(f(a) - p(a)\) ，商多项式距离低次多项式所在的 RS 编码空间就很远了。

注意到这里要求任意的 \(\hat{u} \in \mathrm{List}(f,d,\delta)\) ，都有 \(\hat{u}\) 与 \(p\) 在 \(S\) 上不一致。而用 Out of Domain Sampling 的方法，我们可以将 \(f\) 在 \(\delta\) 范围内的码字以极大概率限制到最多一个，这会使得 Verifier 更容易去检测。我们将在下一小节详细介绍该方法。

\(\mathrm{Quotient}\) 函数可以帮助我们实现在函数 \(f\) 上添加约束。例如想限制 \(f\) 在点 \(a\) 处的值为 \(b\) ，那么可以通过 \(\mathrm{Quotient}(f, \{a\}, p)\) 来实现，其中 \(p(a) = b\) ，即

\[ \mathrm{Quotient}(f, \{a\}, p) = \frac{f(x) - p(x)}{x - a} \]

接着证明 \(\mathrm{Quotient}(f, \{a\}, p) \in \mathrm{RS}[\mathbb{F}, \mathcal{L}, d - 1]\) 就可以了。如果 Prover 提供的 \(f\) 在 \(a\) 点的值不为 \(b\) ，即 \(f(a) \neq b\) ，那么 \(f(a) \neq p(a)\) ，就会导致 \(\mathrm{Quotient}(f, \{a\}, p)\) 距离 \(\mathrm{RS}[\mathbb{F}, \mathcal{L}, d - 1]\) 有 \(\delta\) 远，就容易被 Verifier 检测出来了。这里只添加了一个约束，自然可以添加多个约束，这样就能在 \(f\) 添加约束的同时将测试 \(f\) 转换为测试 \(\mathrm{Quotient}\) 函数距离对应的 RS 编码空间有 \(\delta\) 近了。

\(\mathrm{Quotient}\) 函数和折叠函数一样有 Local 性质。要计算 \(\mathrm{Quotient}\) 函数在点 \(x \in \mathcal{L}\backslash\mathcal{S}\) 的值，通过查询函数 \(f\) 在 \(x\) 点的值就可以计算得出。

Out of Domain Sampling#

Out of Domain Sampling 是一种强大的工具，其可以帮助我们限制 Prover 提供的函数 \(f\) 在 \(\delta\) 范围内的码字数量，这样就就可以将 List Decoding 转换为 Unique Decoding 了。

对于函数 \(f: \mathcal{L} \rightarrow \mathbb{F}\) ，Verifier 从区域 \(\mathcal{L}\) 之外随机选取一个数 \(\alpha \in \mathbb{F} \backslash \mathcal{L}\) ，Prover 返回值 \(\beta\) ，那么在 \(f\) 的 \(\delta\) 范围内的码字列表 \(\mathrm{List}(f,d,\delta)\) 中，大概率最多只有一个码字 \(\hat{u}\) 满足 \(\hat{u}(\alpha) = \beta\) 。

可以用代数基本定理来说明这一点。我们只要证明在 \(\mathrm{List}(f,d,\delta)\) 中存在两个不同的码字 \(\hat{u}'\) 与 \(\hat{u}\) ，它们在 \(\alpha\) 点的值都相等的概率比较小就可以了，这也就说明了大概率最多有一个码字满足 \(\hat{u}(\alpha) = \beta\) 。

先固定两个不同的码字 \(\hat{u}'\) 与 \(\hat{u}\) ，由于它们是不同的码字并且次数都小于 \(d\) ，则由代数基本定理可以得到

\[ \Pr_{\alpha \leftarrow \mathbb{F} \backslash \mathcal{L}} [\hat{u}'(\alpha) = \hat{u}(\alpha)] \le \frac{d - 1}{|\mathbb{F}| - |\mathcal{L}|} \]

假设 \(\mathrm{RS}[\mathbb{F}, \mathcal{L},d]\) 是 \((\delta, l)\) 可列表解码的，意思就是在 \(\delta\) 范围内的码字数量最多为 \(l\) 个，那么任意选取不同的两个码字 \(\hat{u}'\) 与 \(\hat{u}\) 的选法就有 \(\binom{l}{2}\) 种。因此任意选取两个不同的码字 \(\hat{u}'\) 与 \(\hat{u}\) ，它们在 \(\alpha\) 点的值相等的概率不超过 \(\binom{l}{2} \cdot \frac{d - 1}{|\mathbb{F}| - |\mathcal{L}|}\) 。这个概率是非常小的，因此得证。

如何去限制 Prover 发送过来的 \(\beta\) 真的是 \(f\) 在点 \(a\) 处的值呢？用上一小节引入的工具 Quotient 就能做到啦。

深入 STIR 协议的一次迭代#

在这一节中将应用前面提到的三个工具，深入 STIR 协议中的一次迭代。

目标：

  • 初始给定一个函数 \(f\) ，想证明其在 \(\mathrm{RS}[\mathbb{F},\mathcal{L},d]\) 中，其中 \(\mathcal{L} =\langle \omega \rangle\) 。

  • 经过一次迭代后，证明函数 \(f' \in \mathrm{RS}[\mathbb{F},\mathcal{L}',d/k]\) ，其中 \(\mathcal{L}' = \omega \cdot \langle \omega^2 \rangle\) 。

也就是函数 \(f\) 进行了 \(k\) 折，其次数降为 \(d/k\) ，但是一次迭代后的函数 \(f'\) 的 evaluation domain \(\mathcal{L}'\) 的大小并不是缩小 \(k\) 倍，而是 \(2\) 倍。这就是前面提到的 STIR 协议的核心思想，通过提升码率来降低查询复杂度。

关于 evaluation domain \(\mathcal{L} =\langle \omega \rangle\) 与 \(\mathcal{L}' = \omega \cdot \langle \omega^2 \rangle\) ，这里举一个例子来说明。假设 \(\omega^8 = 1\) 。

这样构造的 \(\mathcal{L}'\) 相比 \(\mathcal{L}\) 大小减少了一半，但其实 \(\langle \omega^2 \rangle\) 也能满足减少一半的要求，为什么不选择 \(\mathcal{L}' = \langle \omega^2 \rangle\) 呢？假设我们进行 \(k = 4\) 折，我们能保证 \(\mathcal{L}^4 = \{\omega^4, \omega^8\}\) 与 \(\mathcal{L}' = \{\omega^1, \omega^3,\omega^5, \omega^7\}\) 不相交。这样做的好处是能避免构造 \(\mathcal{L}^4 \cap \mathcal{L}'\) 中的相交点定义的函数 \(\mathrm{Fill}\) ，这样 Verifier 就不用额外检查 \(\mathrm{Fill}\) 的函数值是否正确了([ACFY24] Remark 5.3 说明了这一点)。

一次迭代的协议流程如下图所示：

  1. 取样折叠随机数(Sample folding randomness): Verifier 先从 \(\mathbb{F}\) 中随机选取一个数 \(r^{\mathrm{fold}}\) ，这个随机数将用于折叠函数 \(f\) 。

  2. 发送折叠函数(Send folded function): Prover 发送折叠后的函数 \(g: \mathcal{L}' \rightarrow \mathbb{F}\) 。如果 Prover 是诚实的，那么函数 \(g\) 是多项式 \(\hat{g}\) 在 \(\mathcal{L}'\) 上的 evaluation 。这里 evaluation 的意思就是 \(g\) 与 \(\hat{g}\) 在 \(\mathcal{L}'\) 上的值完全一致，而多项式 \(\hat{g}\) 是通过 \(\mathrm{Fold}(f, r^{\mathrm{fold}})\) 得到的。首先用随机数 \(r^{\mathrm{fold}}\) 对函数 \(f\) 进行 \(k\) 次折叠，得到了 \(\mathrm{Fold}(f, r^{\mathrm{fold}}) : \mathcal{L}^k \rightarrow \mathbb{F}\) ，此时折叠函数的取值范围是 \(\mathcal{L}^k\) ，我们想要的是在 \(\mathcal{L}'\) 上取值，这时只需将 \(\mathrm{Fold}(f, r^{\mathrm{fold}})\) 的定义域扩展(extension) 到 \(\mathcal{L}'\) 上即可，就得到了多项式 \(\hat{g}: \mathcal{L}' \rightarrow \mathbb{F}\) ，其次数小于 \(d/k\) 。

  3. Out-of-domain sample: Verifier 从 \(\mathbb{F}\backslash \mathcal{L}'\) 中取一个随机数 \(r^{\mathrm{out}}\) ，发送给 Prover 。

  4. Out-of-domain reply: Prover 答复 \(\beta \in \mathbb{F}\) 。如果 Prover 是诚实的，那么 \(\beta := \hat{g}(r^{\mathrm{out}})\) 。

📝 Notes 这里第 3 步和第 4 步的目的是为了用 Out of domain Sampling 来将 \(g'\) 在 \(\delta\) 范围内的码字数量限制为最多一个，能将列表解码转换为唯一解码。

  1. Shift queries: Verifier 从 \(\langle \omega^k \rangle\) 中选取 \(t\) 个随机数，即 \(\forall i \in [t],r_i^{\mathrm{shift}} \leftarrow \langle \omega^k \rangle\) 。根据折叠函数的 Local 性质，Verifier 通过查询 \(f\) 可计算得到 \(y_i := f_{\mathrm{fold}}(r_i^{\mathrm{shift}})\) ，其中 \(f_{\mathrm{fold}} :=\mathrm{Fold}(f, r^{\mathrm{fold}})\) 。

在第 2 步中 Prover 发送了 \(g: \mathcal{L}' \rightarrow \mathbb{F}\) 并且 Prover 声称其与 \(\mathrm{Fold}(f, r^{\mathrm{fold}})\) 在 \(\mathcal{L}'\) 上的取值是一致的，但是 Verfier 无法直接查询折叠函数在 \(\mathcal{L}'\) 上的值， Verifier 只能通过查询 \(f\) 的方式来计算得到 \(\mathrm{Fold}(f, r^{\mathrm{fold}})\) 在 \(\mathcal{L}^k\) 上的取值。好在这里可以用到 Quotient 工具来保证一致性。

在第 3 步和第 4 步先用 Out-of-domain Sampling 的方法限制 \(g\) 在 \(\delta\) 范围内的码字数量最多为一个，设为 \(\hat{u}\) ，然后在第 5 步查询 \(\mathrm{Fold}(f, r^{\mathrm{fold}})\) 在 \(\mathcal{L}^k\) 上的值，这里方便后续验证 \(\hat{u}\) 与折叠函数在 \(\mathcal{L}^k\) 上的值是否一致。验证是否一致就交给 Quotient 函数了。

将所有这些要确保一致性的点组成集合 \(\mathcal{G} := \{r^{\mathrm{out}},r_1^{\mathrm{shift}}, \ldots, r_t^{\mathrm{shift}}\}\) ，然后定义函数 \(p: \mathcal{G}\rightarrow \mathbb{F}\) ，其满足：

\[ p(r^{\mathrm{out}}) = \beta, \]
\[ p(r_i^{\mathrm{shift}}) = y_i. \]

定义下一步的函数 \(f'\) 为

\[ f' := \mathrm{Quotient}(f, \mathcal{G}, p) = \frac{g(x) - \hat{p}(x)}{\prod_{a \in \mathcal{G}}(X - a)}. \]

由于 Quotient 函数具有 Local 性质，因此想要计算 \(f'\) 在 \(\mathcal{L}'\) 上的值，只需要查询 \(g\) 在 \(\mathcal{L}'\) 上的值就可以了。

至此，接下来测试 \(f'\) 距离 \(\mathrm{RS}[\mathbb{F},\mathcal{L}',d/k]\) 是否有 \(\delta\) 近就可以了。

细看 \(f'\) 的公式，可以发现 Prover 诚实情况下 \(f' \in \mathrm{RS}[\mathbb{F}, \mathcal{L}', d/k - |\mathcal{G}|]\) ，这里其实出现了多项式次数的降低，需要进行次数校正 (degree correction) ，将 \(f'\) 的次数校正为 \(d/k\) 。关于这一点将在后文进行介绍。

Soundness 分析#

在本小节将对一次迭代进行 soundness 分析，即如果 Prover 作弊， \(f\) 距离 \(\mathrm{RS}[\mathbb{F},\mathcal{L},d]\) 有 \(\delta\) 远，来分析 \(f'\) 距离 \(\mathrm{RS}[\mathbb{F},\mathcal{L}',d/k- |\mathcal{G}|]\) 也比较远的概率。[ACFY24] Lemma 1 给出了如下的结论：

命题 1 [ACFY24, Lemma 1] 如果 \(f\) 距离 \(\mathrm{RS}[\mathbb{F},\mathcal{L},d]\) 有 \(\delta\) 远，那么除了概率为 \((1 - \delta)^t + \mathrm{poly}(|\mathcal{L}|)/|\mathbb{F}|\) 的情况，\(f'\) 距离 \(\mathrm{RS}[\mathbb{F},\mathcal{L}',d/k- |\mathcal{G}|]\) (大约) 有 \((1 - \sqrt{\rho'})\) 远。

证明思路：

  1. 根据折叠函数保持距离的性质，对 \(f\) 用随机数 \(r^{\mathrm{fold}}\) 折叠之后得到的函数 \(f_{r^{\mathrm{fold}}} := \mathrm{Fold}(f, r^{\mathrm{fold}})\) 距离 \(\mathrm{RS}[\mathbb{F},\mathcal{L}^k,d/k]\) 有 \(\delta\) 远的概率超过 \(1 - \mathrm{poly}(|\mathcal{L}|/|\mathbb{F}|)\) 。

  2. 根据 Out-of-domain Sampling 的性质，\(g\) 在 \(1 - \sqrt{\rho'}\) 范围内最多有一个码字 \(\hat{u}\) 满足 \(\hat{u}(r^{\mathrm{out}}) = \beta\) 的概率超过 \(1 - \mathrm{poly}(|\mathcal{L}|)/|\mathbb{F}|\) 。

现在分析下第 2 点，函数 \(g: \mathcal{L}' \rightarrow \mathbb{F}\) ，现在考虑其与编码空间 \(\mathrm{RS}[\mathbb{F}, \mathcal{L}', d/k]\) 的距离。根据 Johnson 界，\(\mathrm{RS}[\mathbb{F}, \mathcal{L}', d/k]\) 是 \((\gamma, l)\) - 可列表解码(list-decodable)的，其中 \(\gamma \approx 1 - \sqrt{\rho'}\) , \(l = \mathrm{poly}(|\mathcal{L}'|) =\mathrm{poly}(|\mathcal{L}|)\) ，也就是最多有 \(l\) 个次数小于 \(d/k\) 的多项式距离 \(g\) 不超过 \(\gamma\) 。那么在 \(l\) 个多项式中任意选取两个不同的多项式 \(\hat{u}'\) 与 \(\hat{u}\) ，从 \(\mathbb{F} \backslash \mathcal{L}'\) 中选取随机数 \(r^{\mathrm{out}}\) ，它们在 \(r^{\mathrm{out}}\) 点的值都等于 \(\beta\) 的概率不超过 \(\frac{d/k - 1}{|\mathbb{F}| - |\mathcal{L}'|}\) 。这两个多项式的选取方法有 \(\binom{l}{2}\) 种，因此这个概率不超过

\[ \binom{l}{2} \cdot \frac{d/k - 1}{|\mathbb{F}| - |\mathcal{L}'|} = O\left(\frac{l^2 \cdot (d/k - 1)}{|\mathbb{F}| - |\mathcal{L}'|}\right) = \mathrm{poly}(|\mathcal{L}|)/|\mathbb{F}|. \]

因此 \(g\) 在 \(1 - \sqrt{\rho'}\) 范围内最多有一个码字 \(\hat{u}\) 满足 \(\hat{u}(r^{\mathrm{out}}) = \beta\) 的概率超过 \(1 - \mathrm{poly}(|\mathcal{L}|)/|\mathbb{F}|\) 。

如果第 1 项和第 2 项都成立，那么这个概率超过 \(1 - \mathrm{poly}(|\mathcal{L}|)/|\mathbb{F}|\) ，现在只需证明 \(f'\) 距离 \(\mathrm{RS}[\mathbb{F},\mathcal{L}',d/k- |\mathcal{G}|]\) (大约) 有 \((1 - \sqrt{\rho'})\) 远的概率至少为 \(1 - (1 - \delta)^t\) 即可。

下面分两种情况进行讨论：

  • 如果在第 2 项中没有码字满足要求，即在 \(g\) 的 \(1 - \sqrt{\rho'}\) 范围内没有码字满足 \(\hat{u}(r^{\mathrm{out}}) = \beta\) ，而根据协议的构造，\(p(r^{\mathrm{out}}) = \beta\) 。因此对于 \(g\) 的 \(1 - \sqrt{\rho'}\) 范围内的任意一个码字有 \(\hat{u}(r^{\mathrm{out}}) \neq p(r^{\mathrm{out}})\) 。由于

    \[ f' := \mathrm{Quotient}(g, \mathcal{G}, p) = \frac{g(x) - \hat{p}(x)}{\prod_{a \in \mathcal{G}}(X - a)}. \]

    根据 Quotient 函数的一致性，此时 \(\hat{u}\) 与 \(p\) 在 \(\mathcal{G}\) 上不完全一致，那么 \(f' = \mathrm{Quotient}(f, \mathcal{G}, p)\) 距离 \(\mathrm{RS}[\mathbb{F},\mathcal{L}',d/k- |\mathcal{G}|]\) 就有 \((1 - \sqrt{\rho'})\) 远。

  • 如果在第 2 项中存在一个码字 \(\hat{u}\) 满足要求，在 \(g\) 的 \(1 - \sqrt{\rho'}\) 范围已经存在了一个码字满足 \(\hat{u}(r^{\mathrm{out}}) = \beta\) 。根据

    \[ f' := \mathrm{Quotient}(g, \mathcal{G}, p) = \frac{g(x) - \hat{p}(x)}{\prod_{a \in \mathcal{G}}(X - a)}. \]

    现在已经满足 \(\hat{u}(r^{\mathrm{out}}) = \beta = p(r^{\mathrm{out}})\) ，如果对于任意的 \(i \in [t]\) ，有 \(\hat{u}(r_i^{\mathrm{shift}}) = y_i = p(r_i^{\mathrm{shift}})\) ，那么 \(f' = \mathrm{Quotient}(f, \mathcal{G}, p)\) 距离 \(\mathrm{RS}[\mathbb{F},\mathcal{L}',d/k- |\mathcal{G}|]\) 不超过 \((1 - \sqrt{\rho'})\) 。否则根据 Quotient 函数的一致性，一旦对于某一个 \(i\) 有 \(\hat{u}(r_i^{\mathrm{shift}}) \neq y_i\) ，此时 \(\hat{u}(r_i^{\mathrm{shift}}) \neq p(r_i^{\mathrm{shift}})\) ，就会导致 \(f'\) 距离 \(\mathrm{RS}[\mathbb{F},\mathcal{L}',d/k- |\mathcal{G}|]\) 有 \((1 - \sqrt{\rho'})\) 远。

    由于第 1 项成立，因此对于折叠函数有 \(\Delta(f_{r^{\mathrm{fold}}}, \mathrm{RS}[\mathbb{F}, \mathcal{L}^k, d/k]) \ge \delta\) ，因此

    \[\begin{split} \begin{aligned} \Pr \left[\forall i \in [t], \hat{u}(r_i^{\mathrm{shift}}) = y_i \right] & = \Pr \left[\forall i \in [t], \hat{u}(r_i^{\mathrm{shift}}) = f_{r^{\mathrm{fold}}}(r_i^{\mathrm{shift}}) \right] \\ & \le (1 - \delta)^t. \end{aligned} \end{split}\]

    因此 \(f'\) 距离 \(\mathrm{RS}[\mathbb{F},\mathcal{L}',d/k- |\mathcal{G}|]\) (大约) 有 \((1 - \sqrt{\rho'})\) 远的概率至少为 \(1 - (1 - \delta)^t\) 。

至此命题 1 得证。 \(\Box\)

实际上，协议的 round-by-round soundness error 大概就为 \(\max \{\frac{\mathrm{poly}(|\mathcal{L}|)}{|\mathbb{F}|}, (1 - \delta)^t\}\) 。

Degree correction#

现在还剩下一个小问题需要解决，那就是根据 \(f'\) 函数的定义

\[ f' := \mathrm{Quotient}(g, \mathcal{G}, p) = \frac{g(x) - \hat{p}(x)}{\prod_{a \in \mathcal{G}}(X - a)}. \]

可以发现，准确来讲，这里是将对 \(f\) 的测试转换为了测试 \(f'\) 到 \(\mathrm{RS}[\mathbb{F},\mathcal{L}',d/k- |\mathcal{G}|]\) 的距离，而不是 \(\mathrm{RS}[\mathbb{F},\mathcal{L}',d/k]\) ，这就需要进行次数校正(degree correction)了。

一般地，不妨假设我们要进行次数校正的函数是 \(f: \mathcal{L} \rightarrow \mathbb{F}\) ，其初始的次数是 \(d\) ，目标矫正的次数是 \(d^* \ge d\) ，我们想要构造一个高效的次数校正算法，能输出一个函数 \(f^*\) 满足：

  1. 如果 \(f \in \mathrm{RS}[\mathbb{F},\mathcal{L},d]\) ，那么 \(f^* \in \mathrm{RS}[\mathbb{F},\mathcal{L},d^*]\) 。

  2. 如果 \(f\) 距离 \(\mathrm{RS}[\mathbb{F},\mathcal{L},d]\) 有 \(\delta\) 远，那么以极大的概率有 \(f^*\) 距离 \(\mathrm{RS}[\mathbb{F},\mathcal{L},d^*]\) 也有 \(\delta\) 远。

  3. 对 \(f^*\) 的查询可以通过查询 \(f\) 来高效的计算出来。

STIR 论文 ([ACFY24], 第 2.3 节) 中提出了一种方法，不仅满足上述三个条件，还利用几何级数求和的方法，使得第 3 项的计算更加高效。

该方法是，随机采样一个域中的元素 \(r \leftarrow \mathbb{F}\) ，定义

\[ f^*(x) = \sum_{i=0}^{e} r^i \cdot f_i(x) \tag{1} \]

其中，\(f_i(x) := x^i \cdot f(x)\) , \(e = d^* - d\) 。将 \((1)\) 式展开可得

\[ f^*(x) = r^0 \cdot x^0 \cdot f(x) + r^1 \cdot x^1 \cdot f(x) + \cdots + r^e \cdot x^e \cdot f(x) \tag{2} \]

根据 \(f^*\) 的构造，自然第 1 项是成立的。

对于 \(\delta < \min \{ 1 - \sqrt{\rho}, 1 - (1 + 1/d^*) \cdot \rho\}\) ，第 2 项也是成立的。这可以通过 [BCIKS20] 中的 Correlated Agreement 定理得到的，这里就不详细展开了。

接下来分析下第 3 项。通过 \((2)\) 式，可以发现如果要计算 \(f^*\) 在 \(x\) 点处的值，当查询到 \(f(x)\) 的值后，要进行 \(e + 1\) 项求和，需要花费 \(O(e)\) 的时间。如果 \(e = \Omega(d)\) ，这是低效的，但是通过几何级数求和的方法，可以将计算复杂度降到 \(O(\log e)\) 。

\[\begin{split} \begin{aligned} f^*(x) & = \sum_{i=0}^{e} r^i \cdot f_i(x) \\ & = \sum_{i=0}^{e} r^i \cdot x^i \cdot f(x)\\ & = f(x) \cdot \sum_{i=0}^{e} (r \cdot x)^i \\ \end{aligned} \end{split}\]

对 \(\sum_{i=0}^{e} (r \cdot x)^i\) 使用几何级数求和公式，可以得到

\[\begin{split} f^*(x) = \begin{cases} f(x) \cdot \frac{1 - (r \cdot x)^{e+1}}{1 - r \cdot x} & \text{if} \quad r \cdot x \neq 1 \\ f(x) \cdot (e + 1) & \text{if} \quad r \cdot x = 1 \end{cases} \end{split}\]

对于比较复杂的 \(f(x) \cdot \frac{1 - (r \cdot x)^{e+1}}{1 - r \cdot x}\) ，其中 \((r \cdot x)^{e+1}\) 这一项可以通过反复平方的方法计算得到，需要 \(O(\log e)\) 次计算，再通过查询 \(f\) 在点 \(x\) 处的值得到 \(f(x)\) ，因此整体需要 \(O(\log e)\) 次操作来计算 \(f^*(x)\) 。

将该方法可以扩展到多个不同次数的函数上。对于 \(m\) 个函数 \(f_1, \ldots, f_m: \mathcal{L} \rightarrow \mathbb{F}\) 以及次数 \(d_1, \ldots, d_m\) ，我们希望进行批量次数校正(batch-degree-correct)，最后得到一个函数 \(f^*\) ，次数为 \(d^*\) 。随机采样一个随机数 \(r \leftarrow \mathbb{F}\) ，定义 \(e_i = d^* - d_i\) 以及

\[ f^*(x) = \sum_{i = 0}^{e_1} r^i \cdot x^i \cdot f_1(x) + r^{1 + e_1} \sum_{i = 0}^{e_2} r^i \cdot x^i \cdot f_2(x) + \cdots + r^{m - 1 + \sum_{j = 1}^{m - 1}e_j} \sum_{i = 0}^{e_m} r^i \cdot x^i \cdot f_m(x). \]

与上面单个函数的次数校正类似，对于 \(\delta < \min \{ 1 - \sqrt{\rho}, 1 - (1 + 1/d^*) \cdot \rho\}\) ，如果有任意的 \(f_i\) 距离 \(\mathrm{RS}[\mathbb{F},\mathcal{L},d_i]\) 有 \(\delta\) 远，那么 \(f^*\) 距离 \(\mathrm{RS}[\mathbb{F},\mathcal{L},d^*]\) 就有 \(\delta\) 远。同样地，用几何级数求和的方式，通过查询 \(f_1, \ldots, f_m\) ，进行 \(O(\sum_i \log e_i) = O(m \cdot \log d^*)\) 次操作就可以计算出 \(f^*\) 在 \(x\) 点的值。

总结#

STIR 通过在每一轮中改变函数的 evaluation domain ，将原来 FRI 协议中的 \(\mathcal{L}^k\) 变为 \(\mathcal{L}'\) ，函数依然是 \(k\) 折，但是 \(\mathcal{L}'\) 只有原来的一半大小，这样做降低了编码空间的码率，能减少 Verifier 的查询数量，这也是 STIR 的核心思想。

在STIR 协议的构造中使用 RS 编码的几个有力的工具，使得整个协议是高效且安全的。

  1. 首先和 FRI 协议一致，先对函数 \(f\) 进行 \(k\) 折，但得到的函数需要将 evaluation domain 从 \(\mathcal{L}^k\) 扩展到 \(\mathcal{L}'\) ，根据折叠函数具有距离保持的性质，这一过程我们可以放心的进行折叠。

  2. 接着为了降低 Verifier 的工作，使用 Out of Domain Sampling 的方式将列表编码的方式转换为唯一解码，也就是协议中 Verifier 从 \(\mathbb{F} \backslash \mathcal{L}\) 中选取一个随机数 \(r^{\mathrm{out}}\) ，要求 Prover 答复 \(\beta\) 。

  3. 此时将 evaluation domain 变为 \(\mathcal{L}'\) 之后，面临的问题是 Verifier 只能查询 \(k\) 折函数 \(\mathrm{f}_{r^{\mathrm{fold}}}\) 在 \(\mathcal{L}^k\) 上的值，好在可以用 Quotient 这个强大的工具来约束 Prover 发送的函数在 \(\mathcal{L}^k\) 上的值与折叠函数在 \(\mathcal{L}^k\) 上的值是一致的。此时 Verifier 从 \(\mathcal{L}^k\) 中选取 \(t\) 个随机数 \(r_{i}^{\mathrm{shift}}\) 进行查询。

  4. 最后结合 \(r^{\mathrm{out}}\) 与 \(r_{i}^{\mathrm{shift}}\) ，用 Quotient 工具来约束 Prover 在这些点发送的值是正确的。

结合这些工具对一次迭代的 STIR 协议进行了 soundness 分析，其实可以得到 STIR 的 round-by-round soundness error 为 \(\max \{\frac{\mathrm{poly}(|\mathcal{L}|)}{|\mathbb{F}|}, (1 - \delta)^t\}\) 。

最后为了将迭代后的 \(f'\) 从次数 \(d/k - |\mathcal{G}|\) 提升到 \(d/k\) ，介绍了利用几何级数求和方法能高效计算的 degree correction 方法。

References#

  • [ACFY24] Gal Arnon, Alessandro Chiesa, Giacomo Fenzi, and Eylon Yogev. “STIR: Reed-Solomon proximity testing with fewer queries.” In Annual International Cryptology Conference, pp. 380-413. Cham: Springer Nature Switzerland, 2024.

  • [BCIKS20] Eli Ben-Sasson, Dan Carmon, Yuval Ishai, Swastik Kopparty, and Shubhangi Saraf. Proximity Gaps for Reed–Solomon Codes. In Proceedings of the 61st Annual IEEE Symposium on Foundations of Computer Science, pages 900–909, 2020.

  • [BCS16] Eli Ben-Sasson, Alessandro Chiesa, and Nicholas Spooner. “Interactive Oracle Proofs”. In: Proceedings of the 14th Theory of Cryptography Conference. TCC ’16-B. 2016, pp. 31–60.

  • [BGKS20] Eli Ben-Sasson, Lior Goldberg, Swastik Kopparty, and Shubhangi Saraf. “DEEP-FRI: Sampling Outside the Box Improves Soundness”. In: Proceedings of the 11th Innovations in Theoretical Computer Science Conference. ITCS ’20. 2020, 5:1–5:32.

  • STIR: Reed–Solomon Proximity Testing with Fewer Queries

  • Video: ZK11: STIR: Reed–Solomon Proximity Testing with Fewer Queries - Gal Arnon & Giacomo Fenzi

Contents