KZG Extractability based on ROM
KZG10 等多项式承诺证明多用于构造 SNA可以看出,Knowledge Soundness 定义的关键在于强调构造提取器算法的可行性,也就是说,如果一个恶意证明者声称在不知道 w w w w w w w w w
**Knowledge Soundness 证明(以 Schnorr 协议为例)**通常我们会将一个 Interactive Oracle Proof 中的多项式 Oracle 用 PCS 编译。 ¶ 考虑到安全性,IOP 本身的 Knowledge Soundness 是容易保证的。然而,对于 IOP 用 PCS 编译之后得到的 SNARK,要证明它的 Knowledge Soundness 性质就没有那么容易了。
相比较于 IOP 中证明者发送包含一整个多项式的 Oracle 在 IOP 模型中,oracle 的长度和多项式是相同的,只不过验证者没有完全读取它),SNARK 中证明者只发送了多项式的承诺,该承诺只包含很少一部分信息:仅仅是多项式在几个点上的取值。
因此,我们只有保证多项式承诺本身是“可提取的“(Extractable),才能够保证 SNARK 的 Knowledge Soundness。(详细论证可以参考 Interactive Oracle Proofs by Eli Ben-Sasson et al.)
不幸的是,Kate 等人并没有证明 KZG10 协议具有 extractability,因此,要把 KZG10 用在构造 SNARK 上,我们必须对其安全性进行重新证明。
一系列之前的工作,包括 Sonic [MBK+19], Plonk [GWC19], Marlin [CHM+19] 提出了基于 non-falsifiable 假设(Knowledge Assumptions)或者基于理想群模型(Idealized Group Model)如GGM,AGM,证明 KZG10 方案 满足 extractability 的方案。可以说,目前大部分基于 KZG 方案构造的 SNARK 系统都间接地依赖理想群模型。
与此同时,SNARK 系统在实现非交互式证明的时候还使用了 Fiat-Shamir 变换,这意味着它们还依赖于另一个强理想化模型,即随机预言机模型(ROM)。这种现状使我们处于一个相当糟糕的境地:我们的 SNARK 系统会同时具有两个模型的缺陷!近些年来,一些论文分别对它们进行了攻击。
而相对于理想群模型来说,ROM 的模型假设更弱(也就意味着安全性更强)。如果能够在 ROM 模型下证明 KZG 方案的安全性,就能够移除 SNARK 系统对理想群模型的依赖,从而增加我们对其安全性的信心。
在这个背景下,Lipmaa,Parisella,Siim 在今年发表了他们的工作 “Constant-Size zk-SNARKs in ROM from Falsifiable Assumptions”(下文简称 [LPS24]),向我们的目标推进了一大步。他们的贡献包括:
基于一个新提出的 falsifiable 假设证明了 KZG 方案在 ROM 模型下的 special soundness 性质 进一步证明了 KZG 方案满足 black-box extractability,以用于编译 IOP 在证明 Plonk 在 ROM 模型下的 knowledge soundness 性质上取得了部分进展 本文中,我们将着重介绍第一点的工作。
Special Soundness ¶ 要介绍 special soundness,我们首先需要了解交互式证明以及其安全定义。
Interactive Proofs and Knowledge Soundness ¶ 【定义1:Public-coin Interactive Proofs】
一个证明目标关系 R R R Π = ( P , V ) \Pi = (P, V) Π = ( P , V ) P , V P,V P , V
证明者输入:公共 statement(记作 x x x w w w 验证者输入:公共 statement(记作 x x x 证明者和验证者进行经过一系列交互,将所有交互的消息合集称为一个 transcript 验证者输出 1 表示接受,0 表示拒绝。 如果在交互中,所有验证者使用的随机数均为公开的,那么我们称该交互式协议为 Public-coin Interactive Proof。此外,假设在整个交互中证明者的发送了 k k k k − 1 k-1 k − 1 ( 2 k − 1 ) (2k-1) ( 2 k − 1 )
众所周知,要保证一个交互式证明是安全的,它需要满足两个安全性质:
Completeness:对于任意一个诚实执行协议的证明者 P P P 存在 w w w ( x , w ) (x,w) ( x , w ) R R R P P P Soundness:对于任意一个可能恶意的证明者,且 不存在 w w w ( x , w ) (x,w) ( x , w ) R R R P P P 上面两个安全性质保证了交互式证明基本的安全性,然而 Soundness 的定义只能够保证某个statement x x x R R R p k pk p k s k sk s k p k = s k ⋅ G pk = sk\cdot G p k = s k ⋅ G p k pk p k G G G G \mathbb{G} G s k sk s k s k sk s k p k ∈ G pk \in \mathbb{G} p k ∈ G
因此我们需要一个更强的安全定义,即 **“**Knowledge Soundness”
【定义2:Knowledge Soundness】
对于一个交互式证明 Π = ( P , V ) \Pi = (P, V) Π = ( P , V ) P ∗ P^* P ∗ x x x w w w ϵ \epsilon ϵ E E E P ∗ P^* P ∗ ϵ ′ \epsilon' ϵ ′ x x x w w w ∣ ϵ ′ − ϵ ∣ |\epsilon'-\epsilon| ∣ ϵ ′ − ϵ ∣ Π \Pi Π
【注】如果一个 Public-coin Interactive Proof 对任意敌手都满足 Completeness 和 Soundness,那么我们称其为 Proof of Knowledge,如果Soundness只对多项式时间敌手满足,那么称其为 Argument of Knowledge。
可以看出,Knowledge Soundness 定义的关键在于强调构造提取器算法的可行性,也就是说,如果一个恶意证明者声称在不知道 w w w w w w w w w
Knowledge Soundness 证明(以 Schnorr 协议为例) ¶ 前文已经给出了较为具体的 Knowledge Soundness 定义,那么我们该如何证明一个交互式证明协议满足该性质呢?显然,最直接的答案是构造一个提取器即可,但如何构造提取器是又是一门很深的学问(直白地说,LPS24 就是在做这件事)。为了方便解释 LPS24 的工作,我们先从一个相对简单的例子入手,来解释 knowledge soundness 的证明思路。
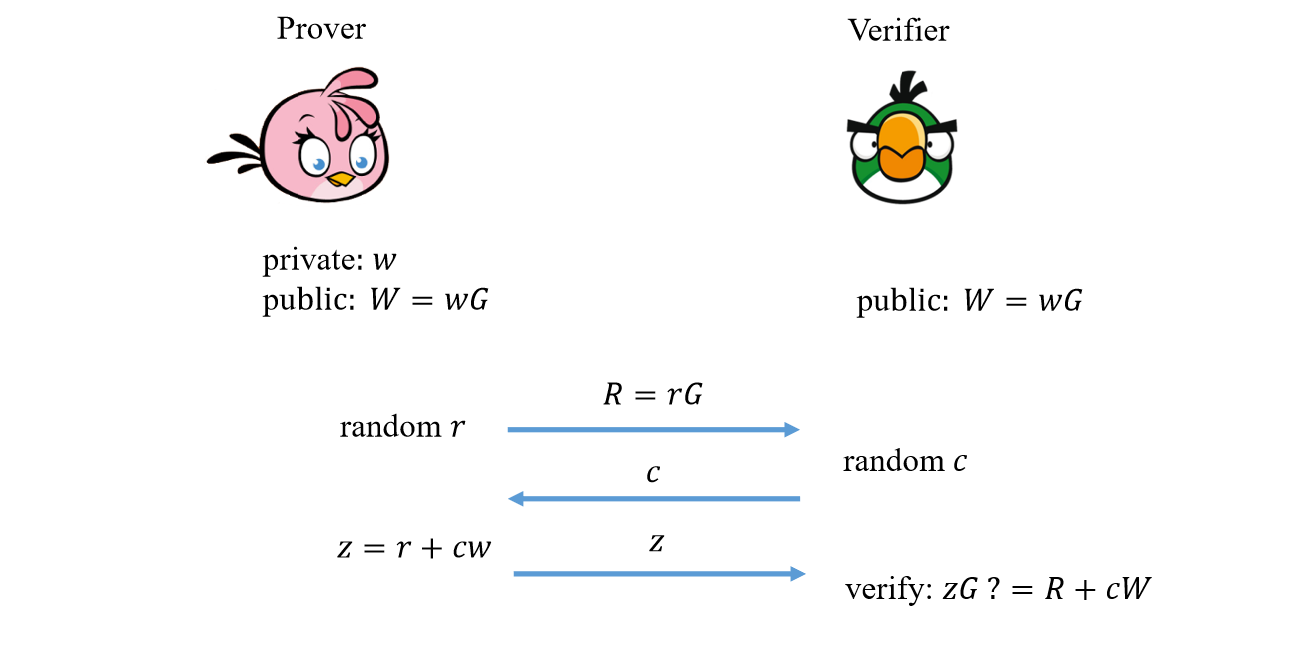
如下图所示 Schnorr 协议 [Sch90] 是一个 3步的交互式证明,在证明者和验证者两方之间进行,通过执行该协议,证明者能够向验证者证明她拥有一个满足离散对数关系 W = w G W=wG W = wG w w w
他们的交互过程如下
证明者生成随机值 r ← F r \leftarrow \mathbb{F} r ← F R = r G R=rG R = r G 验证者生成随机值 c ← F c \leftarrow \mathbb{F} c ← F 证明者计算公开值 z = r + c w z = r+cw z = r + c w 最后验证者根据在协议中收到的消息检查 z G = ? R + c W zG \overset{?}{=} R +cW z G = ? R + c W ( R , c , z ) (R,c,z) ( R , c , z )
很容易证明,Schnorr 协议满足 Completeness 性质,我们在次不过多赘述。
接下来我们重点考虑 Knowledge Soundness 性质:
根据定义2,我们先给出结论:如果存在多项式时间算法 P ∗ P^* P ∗ E E E P ∗ P^* P ∗ w w w
那么该如何构造一个 E E E
首先,我们构造一个子算法 E s s E_{ss} E ss W W W ( R , c 1 , z 1 ) , ( R , c 2 , z 2 ) (R,c_1,z_1), (R,c_2,z_2) ( R , c 1 , z 1 ) , ( R , c 2 , z 2 ) R R R c 1 , c 2 c_1,c_2 c 1 , c 2 w w w W = w G W=wG W = wG 接着,我们构造另一个子算法 E r w E_{rw} E r w E r w E_{rw} E r w P ∗ P^* P ∗ ( R , c 1 , z 1 ) (R, c_1, z_1) ( R , c 1 , z 1 ) E r w E_{rw} E r w P ∗ P^* P ∗ R R R P ∗ P^* P ∗ c 1 c_1 c 1 P ∗ P^* P ∗ ( R , c 2 , z 2 ) (R, c_2, z_2) ( R , c 2 , z 2 ) 最后, E E E E r w E_{rw} E r w E s s E_{ss} E ss w w w 【实现子算法 E s s E_{ss} E ss
子算法 E s s E_{ss} E ss E s s E_{ss} E ss z 1 , z 2 z_1, z_2 z 1 , z 2 P ∗ P^* P ∗
z 1 = r + c 1 w ′ z 2 = r + c 2 w ′ z_1 = r + c_1 w' \\ z_2 = r+c_2w' z 1 = r + c 1 w ′ z 2 = r + c 2 w ′ 解方程能够计算出 w ′ = ( z 1 − z 2 ) / ( c 1 − c 2 ) w' = (z_1-z_2)/(c_1-c_2) w ′ = ( z 1 − z 2 ) / ( c 1 − c 2 ) w ′ G = ? W w'G\overset{?}{=}W w ′ G = ? W E ′ E' E ′ w = w ′ w=w' w = w ′ E ′ E' E ′
( z 1 − z 2 ) c 1 − c 2 G = W \frac{(z_1-z_2)}{c_1-c_2} G = W c 1 − c 2 ( z 1 − z 2 ) G = W 由于破解离散对数假设的概率是可以忽略的,可以得到 E s s E_{ss} E ss P ∗ P^* P ∗
【获取 transcripts】
我们已经实现了第一步,接下来看第二步,其中要求算法 E r w E_{rw} E r w P ∗ P^* P ∗ P ∗ P^* P ∗ ϵ \epsilon ϵ P ∗ P^* P ∗ P ∗ P^* P ∗ E r w E_{rw} E r w P ∗ P^* P ∗ E r w E_{rw} E r w
所以,要顺利完成第二步,我们必须证明以下两点
E r w E_{rw} E r w E r w E_{rw} E r w w w w 从 Knowledge Soundness 到 Special Soundness ¶ 论文 [Cra96] 对 E r w E_{rw} E r w
【Rewinding Lemma】
对于一个3-步交互式证明 Π = ( P , V ) \Pi = (P, V) Π = ( P , V ) P ∗ P^* P ∗ E r w E_{rw} E r w P ∗ P^* P ∗ R R R c c c E r w E_{rw} E r w
Rewinding Lemma 并不局限于 Schnorr-协议,实际上对任何3-步 Sigma 协议,提取器算法 E r w E_{rw} E r w k − 1 k-1 k − 1
因此,Rewinding Lemma 实际上为构建具体协议的研究者们简化了证明 Knowledge Soundness 的过程,对于基于 Sigma 模型下设计的协议,我们通常只需要在安全证明中给出子算法 E s s E_{ss} E ss
定义3:Special Soundness
对于一个3-步交互式证明 Π = ( P , V ) \Pi = (P, V) Π = ( P , V ) E s s E_{ss} E ss x x x ( R , c 1 , z 1 ) , ( R , c 2 , z 2 ) (R,c_1,z_1), (R,c_2,z_2) ( R , c 1 , z 1 ) , ( R , c 2 , z 2 ) w w w Π \Pi Π
【注】上面的定义也称作 2-special soundness,如果提取算法 E E E k k k k k k
随着交互式证明的发展,研究者们也并不局限于只构造3-步协议,为了满足这一需求,Special Soundness 被进一步拓展到 ( 2 n − 1 ) (2n-1) ( 2 n − 1 ) j ∈ [ 1 , n ] j\in[1,n] j ∈ [ 1 , n ] E r w E_{rw} E r w P ∗ P^* P ∗ k j − 1 k_j-1 k j − 1 E s s E_{ss} E ss n n n ( k 1 , . . . , k n ) − (k_1,...,k_n)- ( k 1 , ... , k n ) − ( k 1 , . . . , k n ) − (k_1,...,k_n)- ( k 1 , ... , k n ) − k k k
LPS24: KZG10 with Special Soundness ¶ 我们在之前的文章中已经介绍了 KZG10 多项式承诺方案的基本流程,在 [LPS24] 中,作者首先将 KZG10 方案写成符合交互式证明的形式,其中证明者拥有公共输入 c k = ( p , [ ( σ i ) i = 0 n ] 1 , [ 1 , σ ] 2 ) ck = (p, [(\sigma^i)_{i=0}^n]_1, [1,\sigma]_2) c k = ( p , [( σ i ) i = 0 n ] 1 , [ 1 , σ ] 2 ) p ← P g e n ( 1 λ ) p \leftarrow Pgen(1^{\lambda}) p ← P g e n ( 1 λ ) S R S SRS SRS f ( X ) f(X) f ( X ) c k ck c k
证明者计算多项式承诺 C = [ f ( σ ) ] 1 C = [f(\sigma)]_1 C = [ f ( σ ) ] 1 验证者选择随机 r r r 证明者计算并发送取值 v = f ( r ) v = f(r) v = f ( r ) π = [ q ( σ ) ] 1 \pi = [q(\sigma)]_1 π = [ q ( σ ) ] 1 q ( X ) = ( f ( X ) − v ) / ( X − r ) q(X) = (f(X)-v)/(X-r) q ( X ) = ( f ( X ) − v ) / ( X − r ) 验证者根据交互数据检查 e ( C − [ v ] 1 , [ 1 ] 2 ) = ? e ( π , [ σ − r ] 2 ) e(C-[v]_1, [1]_2) \overset{?}{=} e(\pi, [\sigma-r]_2) e ( C − [ v ] 1 , [ 1 ] 2 ) = ? e ( π , [ σ − r ] 2 )
类似的我们将双方之间的交互消息集合称作 transcript,如果某个transcript t r tr t r n + 1 n+1 n + 1 t r ⃗ \vec{tr} t r
t r ⃗ \vec{tr} t r C C C 对任意两个 transcript t r i , t r j , i , j ∈ [ 0 , n ] tr_i, tr_j, i,j\in [0,n] t r i , t r j , i , j ∈ [ 0 , n ] r i ≠ r j r_i \neq r_j r i = r j 除了定义交互形式的 KZG10 方案,[LPS24] 的作者还提出了一种新的困难问题假设,名为 Adaptive Rational Strong Diffie-Hellman 假设,简称 ARSDH 假设,其定义如下
【( n + 1 ) (n+1) ( n + 1 )
如果对于任何多项式时间敌手算法 A A A p ← P g e n ( 1 λ ) p \leftarrow Pgen(1^{\lambda}) p ← P g e n ( 1 λ ) σ \sigma σ ( [ ( σ i ) i = 0 n ] 1 , [ 1 , σ ] 2 ) ([(\sigma^i)_{i=0}^n]_1, [1,\sigma]_2) ([( σ i ) i = 0 n ] 1 , [ 1 , σ ] 2 ) A A A [ g ] 1 , [ φ ] 1 [g]_1, [\varphi]_1 [ g ] 1 , [ φ ] 1 n + 1 n+1 n + 1 S S S
[ g ] 1 ≠ [ 0 ] 1 ∧ e ( [ g ] 1 , [ 1 ] 2 ) = e ( [ φ ] 1 , [ Z S ( σ ) ] 2 ) [g]_1 \neq [0]_1 \wedge e([g]_1, [1]_2) = e([\varphi]_1, [Z_S(\sigma)]_2) [ g ] 1 = [ 0 ] 1 ∧ e ([ g ] 1 , [ 1 ] 2 ) = e ([ φ ] 1 , [ Z S ( σ ) ] 2 ) 如果 A A A ( n + 1 ) (n+1) ( n + 1 ) p ← P g e n ( 1 λ ) p \leftarrow Pgen(1^{\lambda}) p ← P g e n ( 1 λ )
ARSDH 是对一个已知的假设 RSDH 的放宽,RSDH 中要求 A A A S S S ( n + 1 ) (n+1) ( n + 1 ) ( n + 1 ) (n+1) ( n + 1 )
( n + 1 ) -ARSDH → ( n + 1 ) -SDH → KZG10’s binding (n+1)\text{-ARSDH} \rightarrow (n+1)\text{-SDH} \rightarrow \text{KZG10's binding} ( n + 1 ) -ARSDH → ( n + 1 ) -SDH → KZG10’s binding 预备知识已经介绍完毕,接下来,我们按照前文介绍的 Schnorr 协议的证明思路,首先给出基于 transcripts 的提取器算法 E s s E_{ss} E ss
Special Soundness of KZG ¶ 首先给出定义:
对于一个多项式承诺方案 P C PC PC E s s E_{ss} E ss c k ck c k n + 1 n+1 n + 1 t r ⃗ \vec{tr} t r
任意 t r j ∈ t r ⃗ tr_j \in \vec{tr} t r j ∈ t r t r ⃗ \vec{tr} t r C C C r r r E E E f ( X ) f(X) f ( X ) C = C o m ( c k ; f ) ∧ f ( r j ) = v j , ∀ j ∈ [ 0 , n ] C = \mathrm{Com}(ck; f) \wedge f(r_j) = v_j, \forall j \in [0,n] C = Com ( c k ; f ) ∧ f ( r j ) = v j , ∀ j ∈ [ 0 , n ] P C PC PC ( n + 1 ) (n+1) ( n + 1 )
显然,设计 E s s E_{ss} E ss t r ⃗ \vec{tr} t r f ′ ( X ) f'(X) f ′ ( X ) f ′ ( X ) f'(X) f ′ ( X ) ( n + 1 ) -ARSDH (n+1)\text{-ARSDH} ( n + 1 ) -ARSDH
我们不妨将每个 t r j tr_j t r j
e ( C − [ v 0 ] 1 , [ 1 ] 2 ) = e ( π 0 , [ σ − r 0 ] 2 ) ⋮ e ( C − [ v n ] 1 , [ 1 ] 2 ) = e ( π n , [ σ − r n ] 2 ) e({\color{red} C-[v_0]_1}, [1]_2) = e({\color{blue}\pi_0}, [\sigma-r_0]_2) \\ \vdots \\ e({\color{red}C-[v_n]_1}, [1]_2) = e({\color{blue}\pi_n}, [\sigma-r_n]_2) e ( C − [ v 0 ] 1 , [ 1 ] 2 ) = e ( π 0 , [ σ − r 0 ] 2 ) ⋮ e ( C − [ v n ] 1 , [ 1 ] 2 ) = e ( π n , [ σ − r n ] 2 ) 令 I = [ 0 , n ] I = [0,n] I = [ 0 , n ] L 0 ( X ) , … , L n ( X ) L_0(X),\ldots,L_n(X) L 0 ( X ) , … , L n ( X ) I I I S = { v i } i ∈ I S=\{v_i\}_{i\in I} S = { v i } i ∈ I L j ( X ) L_j(X) L j ( X )
L j ( X ) = ∏ i ∈ I / { j } ( X − r i ) ∏ i ∈ I / { j } ( r j − r i ) \color{purple} L_j(X) = \frac{\prod_{i\in I/\{j\}} (X-r_i)}{\prod_{i\in I/\{j\}} (r_j-r_i)} L j ( X ) = ∏ i ∈ I / { j } ( r j − r i ) ∏ i ∈ I / { j } ( X − r i ) 现在,将每个验证关系等式两边同时乘上 Lagrange 多项式在 σ \sigma σ j ∈ [ 0 , n ] j\in[0,n] j ∈ [ 0 , n ]
e ( C − [ v j ] 1 , [ 1 ] 2 ) ⋅ L j ( σ ) = e ( π j , [ σ − r j ] 2 ) ⋅ L j ( σ ) e({\color{red}C-[v_j]_1}, [1]_2)\cdot {\color{purple}L_j(\sigma)} = e({\color{blue}\pi_j}, [\sigma-r_j]_2) \cdot {\color{purple}L_j(\sigma)} e ( C − [ v j ] 1 , [ 1 ] 2 ) ⋅ L j ( σ ) = e ( π j , [ σ − r j ] 2 ) ⋅ L j ( σ ) e ( C − [ v j ] 1 , [ 1 ] 2 ) ⋅ L j ( σ ) = e ( π j ⋅ ∏ i ∈ I / { j } ( σ − r i ) ∏ i ∈ I / { j } ( r j − r i ) , [ σ − r j ] 2 ) e({\color{red}C-[v_j]_1}, [1]_2)\cdot {\color{purple}L_j(\sigma)} = e({\color{blue}\pi_j} \cdot {\color{purple} \frac{\prod_{i\in I/\{j\}} (\sigma-r_i)}{\prod_{i\in I/\{j\}} (r_j-r_i)}}, [\sigma-r_j]_2) e ( C − [ v j ] 1 , [ 1 ] 2 ) ⋅ L j ( σ ) = e ( π j ⋅ ∏ i ∈ I / { j } ( r j − r i ) ∏ i ∈ I / { j } ( σ − r i ) , [ σ − r j ] 2 ) $$
e({\color{red}C-[v_j]_1}, [1]2)\cdot {\color{purple}L_j(\sigma)} = e({\color{blue}\pi_j} \cdot {\color{purple} \frac{1}{\prod {i\in I/{j}} (r_j-r_i)}}, [Z_S(\sigma)]_2) $$
并将所有 n + 1 n+1 n + 1
e ( ∑ j ∈ I ( C − [ v j ] 1 ) ⋅ L j ( σ ) , [ 1 ] 2 ) = e ( ∑ j ∈ I π j ⋅ 1 ∏ i ∈ I / { j } ( r j − r i ) , [ Z S ( σ ) ] 2 ) e(\sum_{j \in I}{\color{red}(C-[v_j]_1)}\cdot {\color{purple}L_j(\sigma)}, [1]_2) = e(\sum_{j \in I} {\color{blue}\pi_j} \cdot {\color{purple} \frac{1}{\prod_{i\in I/\{j\}} (r_j-r_i)}}, [Z_S(\sigma)]_2) e ( j ∈ I ∑ ( C − [ v j ] 1 ) ⋅ L j ( σ ) , [ 1 ] 2 ) = e ( j ∈ I ∑ π j ⋅ ∏ i ∈ I / { j } ( r j − r i ) 1 , [ Z S ( σ ) ] 2 ) 令 ∑ j ∈ I [ v j ] 1 ⋅ L j ( σ ) = [ L ( σ ) ] 1 \sum_{j \in I} {\color{red} [v_j]_1} \cdot {\color{purple} L_j(\sigma)} = [{\color{purple} L(\sigma)}]_1 ∑ j ∈ I [ v j ] 1 ⋅ L j ( σ ) = [ L ( σ ) ] 1
L H S = e ( C − ∑ j ∈ I [ v j ] 1 ⋅ L j ( σ ) , [ 1 ] 2 ) = e ( C − [ L ( σ ) ] 1 , [ 1 ] 2 ) LHS = e({\color{red}C}-\sum_{j \in I}{\color{red} [v_j]_1}\cdot {\color{purple}L_j(\sigma)}, [1]_2) \\ = e({\color{red}C}-{\color{purple}[L(\sigma)]_1}, [1]_2) L H S = e ( C − j ∈ I ∑ [ v j ] 1 ⋅ L j ( σ ) , [ 1 ] 2 ) = e ( C − [ L ( σ ) ] 1 , [ 1 ] 2 ) 令 ∑ j ∈ I ( π j / ∏ i ∈ I / { j } ( r j − r i ) ) = φ \sum_{j\in I} \left( {\color{blue} \pi_j} / {\color{purple} \prod_{i\in I/\{j\}}(r_j -r_i)} \right) = {\color{blue} \varphi} ∑ j ∈ I ( π j / ∏ i ∈ I / { j } ( r j − r i ) ) = φ
R H S = e ( ∑ j ∈ I π j ⋅ 1 ∏ i ∈ I / { j } ( r j − r i ) , [ Z S ( σ ) ] 2 ) = e ( [ ∑ j ∈ I q j ( σ ) ∏ i ∈ I / { j } ( r j − r i ) ] 1 , [ Z S ( σ ) ] 2 ) = e ( [ φ ] 1 , [ Z S ( σ ) ] 2 ) RHS = e(\sum_{j \in I} {\color{blue}\pi_j} \cdot {\color{purple} \frac{1}{\prod_{i\in I/\{j\}} (r_j-r_i)}}, [Z_S(\sigma)]_2) \\ = e([\sum_{j\in I} \frac{\color{blue} q_j(\sigma)}{\color{purple} \prod_{i \in I/\{j\}}(r_j-r_i)}]_1, [Z_S(\sigma)]_2) \\ = e([{\color{blue} \varphi}]_1, [Z_S(\sigma)]_2) R H S = e ( j ∈ I ∑ π j ⋅ ∏ i ∈ I / { j } ( r j − r i ) 1 , [ Z S ( σ ) ] 2 ) = e ([ j ∈ I ∑ ∏ i ∈ I / { j } ( r j − r i ) q j ( σ ) ] 1 , [ Z S ( σ ) ] 2 ) = e ([ φ ] 1 , [ Z S ( σ ) ] 2 ) 最终得到等式
L H S = e ( C − [ L ( σ ) ] 1 , [ 1 ] 2 ) = e ( [ φ ] 1 , [ Z S ( σ ) ] 2 ) = R H S LHS = e({\color{red}C}-{\color{purple}[L(\sigma)]_1}, [1]_2) = e([{\color{blue} \varphi}]_1, [Z_S(\sigma)]_2) = RHS L H S = e ( C − [ L ( σ ) ] 1 , [ 1 ] 2 ) = e ([ φ ] 1 , [ Z S ( σ ) ] 2 ) = R H S 基于该等式,提取算法 E s s E_{ss} E ss n + 1 n+1 n + 1 v 0 , … , v n v_0,\ldots,v_n v 0 , … , v n L ( X ) {\color{purple} L(X)} L ( X ) [ L ( σ ) ] 1 = [ ∑ j ∈ I v j ⋅ L j ( σ ) ] 1 [{\color{purple} L(\sigma)}]_1 = [\sum_{j\in I}v_j \cdot L_j(\sigma)]_1 [ L ( σ ) ] 1 = [ ∑ j ∈ I v j ⋅ L j ( σ ) ] 1 [ L ( σ ) ] 1 = ? C [{\color{purple} L(\sigma)}]_1 \overset{?}{=} {\color{red} C} [ L ( σ ) ] 1 = ? C
如果 [ L ( σ ) ] 1 = C [{\color{purple} L(\sigma)}]_1 = {\color{red} C} [ L ( σ ) ] 1 = C E s s E_{ss} E ss L ( X ) {\color{purple} L(X)} L ( X )
如果 [ L ( σ ) ] 1 ≠ C [{\color{purple} L(\sigma)}]_1 \neq {\color{red} C} [ L ( σ ) ] 1 = C E s s E_{ss} E ss L ( X ) {\color{purple} L(X)} L ( X ) ( n + 1 ) -ARSDH (n+1)\text{-ARSDH} ( n + 1 ) -ARSDH
E s s E_{ss} E ss [ g ] 1 = C − [ L ( σ ) ] 1 , {\color{red} [g]_1} = {\color{red} C}-[{\color{purple} L(\sigma)}]_1, [ g ] 1 = C − [ L ( σ ) ] 1 , [ g ] 1 , [ φ ] 1 {\color{red} [g]_1}, [{\color{blue} \varphi}]_1 [ g ] 1 , [ φ ] 1 ( n + 1 ) -ARSDH (n+1)\text{-ARSDH} ( n + 1 ) -ARSDH 显然,上述实例满足 e ( [ g ] 1 , [ 1 ] 2 ) = e ( [ φ ] 1 , [ Z S ( σ ) ] 2 ) e({\color{red} [g]_1}, [1]_2) = e([{\color{blue} \varphi}]_1, [Z_S(\sigma)]_2) e ( [ g ] 1 , [ 1 ] 2 ) = e ([ φ ] 1 , [ Z S ( σ ) ] 2 ) 证明完毕。
Rewinding Lemma ¶ 上述证明保证了 KZG10 满足 ( n + 1 ) (n+1) ( n + 1 ) E r w E_{rw} E r w n + 1 n+1 n + 1
具体来说,对于如下 E r w E_{rw} E r w
E r w E_{rw} E r w r r r P ∗ P^* P ∗ t r 0 tr_0 t r 0 检查 t r 0 tr_0 t r 0 r ′ r' r ′ E r w E_{rw} E r w r r r P ∗ P^* P ∗ E r w E_{rw} E r w ( n + 1 ) (n+1) ( n + 1 ) E r w E_{rw} E r w r r r ( n + 1 ) (n+1) ( n + 1 ) [LPS24] 论文中采取了和 [ACK21] 相同的证明思路,令 H H H { r ⃗ = ( r p , r c k , r A ) ∈ { 0 , 1 } p o l y ( λ ) } \{ \vec{r} = ( r_p, r_{ck}, r_A) \in \{ 0,1 \}^{poly(\lambda)} \} { r = ( r p , r c k , r A ) ∈ { 0 , 1 } p o l y ( λ ) } r p , r c k , r A r_p, r_{ck},r_A r p , r c k , r A P g e n Pgen P g e n S R S SRS SRS H H H F \mathbb{F} F P ∗ P^* P ∗ r ⃗ \vec{r} r r r r H H H H [ r ⃗ ] [ r ] = 1 H[\vec{r}][r] = 1 H [ r ] [ r ] = 1
接下来,我们分别对 E r w E_{rw} E r w
【概率分析】
定义事件如下:
事件 A:t r 0 tr_0 t r 0 事件 B:∀ j ∈ [ 1 , n ] \forall j \in [1,n] ∀ j ∈ [ 1 , n ] t r j tr_j t r j 那么 E r w E_{rw} E r w A → B A \rightarrow B A → B
P r [ A → B ] = P r [ A ∧ ( A → B ) ] + P r [ ¬ A ∧ ( A → B ) ] = P r [ A ∧ B ] + P r ( ¬ A ) Pr[A \rightarrow B] = Pr[A \wedge (A \rightarrow B)] + Pr[\neg{A} \wedge (A \rightarrow B)] \\ = Pr[A \wedge B] + Pr(\neg{A}) P r [ A → B ] = P r [ A ∧ ( A → B )] + P r [ ¬ A ∧ ( A → B )] = P r [ A ∧ B ] + P r ( ¬ A ) 【注】:A → B A \rightarrow B A → B
A A A B B B A → B A \rightarrow B A → B T T T T F F F T T F F T
考虑概率 P r [ A ∧ B ] Pr[A \wedge B] P r [ A ∧ B ] A ∧ B A \wedge B A ∧ B P ∗ P^* P ∗ r ⃗ \vec{r} r t r 0 tr_0 t r 0 r ⃗ \vec{r} r H [ r ⃗ ] H[\vec{r}] H [ r ] n + 1 n+1 n + 1
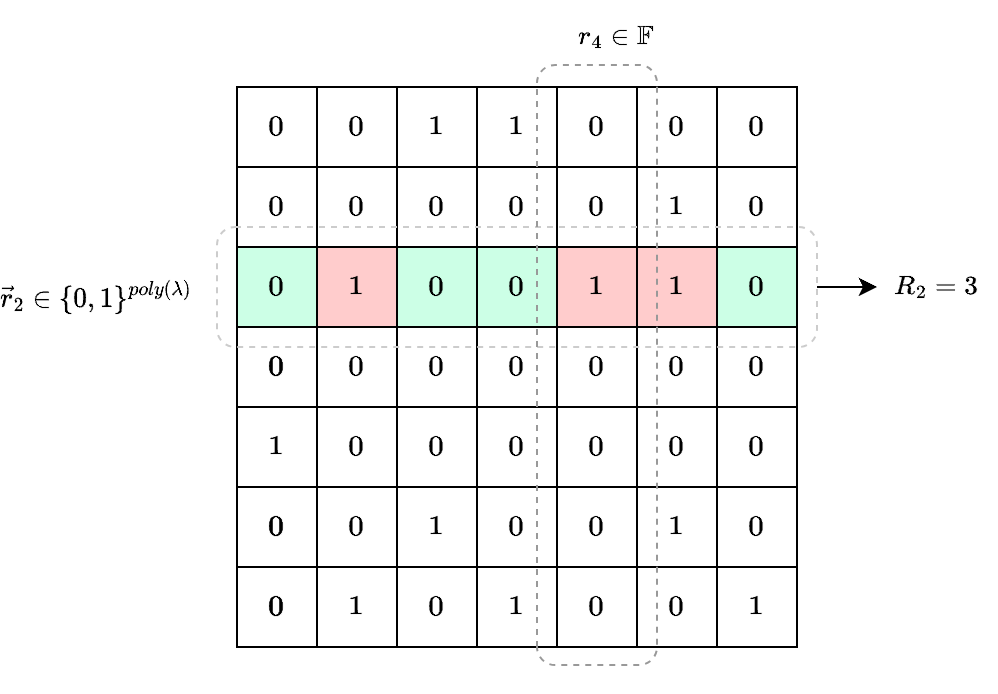
不妨设 R j R_j R j H H H j j j R 2 = 3 R_2 = 3 R 2 = 3 ≥ n + 1 \ge n+1 ≥ n + 1 ∑ j = n + 1 ∣ F ∣ j ⋅ R j \sum_{j=n+1}^{|\mathbb{F}|} j \cdot R_j ∑ j = n + 1 ∣ F ∣ j ⋅ R j P r [ A ∧ B ] Pr[A \wedge B] P r [ A ∧ B ]
P r [ A ∧ B ] = ∑ j = n + 1 ∣ F ∣ j ⋅ R j ∣ r ⃗ ∣ ⋅ ∣ F ∣ = ∑ j = 0 ∣ F ∣ j ⋅ R j ∣ r ⃗ ∣ ⋅ ∣ F ∣ − ∑ j = 0 n j ⋅ R j ∣ r ⃗ ∣ ⋅ ∣ F ∣ = P r [ A ] − ∑ j = 0 n j ⋅ R j ∣ r ⃗ ∣ ⋅ ∣ F ∣ Pr[A \wedge B]=\frac{\sum_{j=n+1}^{|\mathbb{F}|} j \cdot R_j }{|\vec{r}|\cdot |\mathbb{F}|} \\ =\frac{\sum_{j=0}^{|\mathbb{F}|} j \cdot R_j }{|\vec{r}|\cdot |\mathbb{F}|} - \frac{\sum_{j=0}^{n} j \cdot R_j }{|\vec{r}|\cdot |\mathbb{F}|} \\= Pr[A] - \frac{\sum_{j=0}^{n} j \cdot R_j }{|\vec{r}|\cdot |\mathbb{F}|} P r [ A ∧ B ] = ∣ r ∣ ⋅ ∣ F ∣ ∑ j = n + 1 ∣ F ∣ j ⋅ R j = ∣ r ∣ ⋅ ∣ F ∣ ∑ j = 0 ∣ F ∣ j ⋅ R j − ∣ r ∣ ⋅ ∣ F ∣ ∑ j = 0 n j ⋅ R j = P r [ A ] − ∣ r ∣ ⋅ ∣ F ∣ ∑ j = 0 n j ⋅ R j 又因为 ∑ j = 0 n j ⋅ R j = ∑ j = 1 n j ⋅ R j ≤ ∑ j = 1 n n ⋅ R j ≤ n ∣ r ⃗ ∣ \sum_{j=0}^{n} j \cdot R_j = \sum_{j=1}^{n} j \cdot R_j \leq \sum_{j=1}^{n} n \cdot R_j \leq n|\vec{r}| ∑ j = 0 n j ⋅ R j = ∑ j = 1 n j ⋅ R j ≤ ∑ j = 1 n n ⋅ R j ≤ n ∣ r ∣
可以得到 P r [ A ∧ B ] Pr[A \wedge B] P r [ A ∧ B ]
P r [ A ∧ B ] ≥ P r [ A ] − n ∣ r ⃗ ∣ ∣ r ⃗ ∣ ∣ F ∣ = P r [ A ] − n ∣ F ∣ Pr[A \wedge B] \ge Pr[A] - \frac{n|\vec{r}|}{|\vec{r}||\mathbb{F}|} = Pr[A] - \frac{n}{|\mathbb{F}|} P r [ A ∧ B ] ≥ P r [ A ] − ∣ r ∣∣ F ∣ n ∣ r ∣ = P r [ A ] − ∣ F ∣ n 最后得到 E r w E_{rw} E r w
P r [ A → B ] = P r [ A ∧ B ] + P r ( ¬ A ) ≥ P r [ A ] − n ∣ F ∣ + P r [ ¬ A ] = 1 − n ∣ F ∣ Pr[A \rightarrow B] = Pr[A \wedge B] + Pr(\neg{A}) \\ \ge Pr[A] - \frac{n}{|\mathbb{F}|} + Pr[\neg A] \\ = 1-\frac{n}{|\mathbb{F}|} P r [ A → B ] = P r [ A ∧ B ] + P r ( ¬ A ) ≥ P r [ A ] − ∣ F ∣ n + P r [ ¬ A ] = 1 − ∣ F ∣ n 【运行时间分析】
对于 E r w E_{rw} E r w P ∗ P^* P ∗ P ∗ P^* P ∗ E r w E_{rw} E r w P ∗ P^* P ∗ Q Q Q E r w E_{rw} E r w p o l y ( λ ) ⋅ Q poly(\lambda)\cdot Q p o l y ( λ ) ⋅ Q
考虑 E r w E_{rw} E r w t r 0 tr_0 t r 0 A A A E r w E_{rw} E r w E r w E_{rw} E r w P ∗ P^* P ∗ Q Q Q
我们先单独讨论计算循环次数这个问题:给定一个随机参数 r ⃗ \vec{r} r H H H H [ r ⃗ ] H[\vec{r}] H [ r ] δ r ⃗ ∣ F ∣ \delta_{\vec{r}}|\mathbb{F}| δ r ∣ F ∣ ∣ F ∣ |\mathbb{F}| ∣ F ∣ H [ r ⃗ ] H[\vec{r}] H [ r ] H [ r ⃗ ] H[\vec{r}] H [ r ] t r 0 tr_0 t r 0 E r w E_{rw} E r w ∣ F ∣ − 1 |\mathbb{F}|-1 ∣ F ∣ − 1 n n n
要计算 Q Q Q
**NHG 分布:**给定一个包含 N N N K K K k ≤ K k\leq K k ≤ K X X X X X X E [ N H G N , K , k ] = k ( N + 1 ) / ( K + 1 ) E[NHG_{N,K,k}] = k(N+1)/(K+1) E [ N H G N , K , k ] = k ( N + 1 ) / ( K + 1 )
相应的,当 H [ r ⃗ ] H[\vec{r}] H [ r ] n n n Q Q Q H [ r ⃗ ] H[\vec{r}] H [ r ] δ r ⃗ ∣ F ∣ \delta_{\vec{r}}|\mathbb{F}| δ r ∣ F ∣ Q Q Q
H [ r ⃗ ] H[\vec{r}] H [ r ] n + 1 n+1 n + 1 E [ Q ∣ A ∧ r ⃗ ] = E [ N H G N , K , k ] + 1 = n / δ r ⃗ + 1 E[Q|A \wedge \vec{r}] = E[NHG_{N,K,k}] + 1 = n/\delta_{\vec{r}} + 1 E [ Q ∣ A ∧ r ] = E [ N H G N , K , k ] + 1 = n / δ r + 1 N = F − 1 , K = δ r ⃗ ∣ F ∣ − 1 , k = n N = \mathbb{F}-1, K = \delta_{\vec{r}}|\mathbb{F}|-1, k=n N = F − 1 , K = δ r ∣ F ∣ − 1 , k = n H [ r ⃗ ] H[\vec{r}] H [ r ] n + 1 n+1 n + 1 δ r ⃗ ∣ F ∣ ≤ n \delta_{\vec{r}}|\mathbb{F}| \leq n δ r ∣ F ∣ ≤ n E r w E_{rw} E r w H [ r ⃗ ] H[\vec{r}] H [ r ] E [ Q ∣ A ∧ r ⃗ ] = ∣ F ∣ ≤ n / δ r ⃗ E[Q|A \wedge \vec{r}] = |\mathbb{F}| \leq n/\delta_{\vec{r}} E [ Q ∣ A ∧ r ] = ∣ F ∣ ≤ n / δ r 上面考虑的是事件 A A A r ⃗ \vec{r} r H [ r ⃗ ] H[\vec{r}] H [ r ] δ r ⃗ ∣ F ∣ \delta_{\vec{r}}|\mathbb{F}| δ r ∣ F ∣ A A A P r [ A ] = δ r ⃗ Pr[A] = \delta_{\vec{r}} P r [ A ] = δ r
E [ Q ∣ r ⃗ ] = E [ Q ∣ A ∧ r ⃗ ] ⋅ P r [ A ] + E [ Q ∣ ¬ A ∧ r ⃗ ] ⋅ P r [ ¬ A ] ≤ n δ r ⃗ ⋅ δ r ⃗ + 1 ⋅ ( 1 − δ r ⃗ ) = n + 1 − δ r ⃗ ≤ n + 1 E[Q|\vec{r}] = E[Q|A \wedge \vec{r}]\cdot Pr[A] + E[Q|\neg A \wedge \vec{r}]\cdot Pr[\neg A] \\ \leq \frac{n}{\delta_{\vec{r}}}\cdot \delta_{\vec{r}} + 1\cdot (1-\delta_{\vec{r}}) = n+1- \delta_{\vec{r}} \leq n+1 E [ Q ∣ r ] = E [ Q ∣ A ∧ r ] ⋅ P r [ A ] + E [ Q ∣¬ A ∧ r ] ⋅ P r [ ¬ A ] ≤ δ r n ⋅ δ r + 1 ⋅ ( 1 − δ r ) = n + 1 − δ r ≤ n + 1 对于所有 r ⃗ ∈ { 0 , 1 } p o l y ( λ ) \vec{r} \in \{ 0,1 \}^{poly(\lambda)} r ∈ { 0 , 1 } p o l y ( λ ) Q Q Q
E [ Q ] = ∑ r ⃗ E [ Q ∣ r ⃗ ] ⋅ P r [ r ⃗ ] ≤ ∑ 1 ∣ r ⃗ ∣ n + 1 ∣ r ⃗ ∣ = n + 1 E[Q] = \sum_{\vec{r}} E[Q|\vec{r}]\cdot Pr[\vec{r}] \leq \sum_{1}^{|\vec{r}|} \frac{n+1}{|\vec{r}|} = n+1 E [ Q ] = r ∑ E [ Q ∣ r ] ⋅ P r [ r ] ≤ 1 ∑ ∣ r ∣ ∣ r ∣ n + 1 = n + 1 证明完毕。
参考文献 ¶ [CHM+19] Chiesa, Alessandro, Yuncong Hu, Mary Maller, et al. “Marlin: Preprocessing zkSNARKs with Universal and Updatable SRS.” Cryptology ePrint Archive (2019). https://
[MBK+19] Maller Mary, Sean Bowe, Markulf Kohlweiss, et al. "Sonic: Zero-Knowledge SNARKs from Linear-Size Universal and Updatable Structured Reference Strings.” Cryptology ePrint Archive (2019). https://
[GWC19] Ariel Gabizon, Zachary J. Williamson, Oana Ciobotaru. “PLONK: Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge.” Cryptology ePrint Archive (2019). https://
[LPS24] Helger Lipmaa, Roberto Parisella, Janno Siim. “Constant-Size zk-SNARKs in ROM from Falsifiable Assumptions.” Cryptology ePrint Archive (2024). https://
[ACK21] Thomas Attema, Ronald Cramer, and Lisa Kohl “A Compressed Sigma-Protocol Theory for Lattices” Cryptology ePrint Archive (2021). https://
[Sch90] Claus-Peter Schnorr. “Efficient identification and signatures for smart cards.” In Gilles Brassard, editor, CRYPTO’89, volume 435 of LNCS, pages 239–252. Springer, Heidelberg, August 1990.
[Cra96] Ronald Cramer. “Modular Design of Secure yet Practical Cryptographic Protocols”. PhD thesis, CWI and University of Amsterdam, 1996.